|
|
This review is a part of the Ferromagnetic Semiconductor Spintronic Web Project.
|
Abstract The body of research on (III,Mn)V diluted magnetic semiconductors (DMSs) initiated during the 1990s has concentrated on three major fronts: (i) the microscopic origins and fundamental physics of the ferromagnetism that occurs in these systems, (ii) the materials science of growth and defects, and (iii) the development of spintronic devices with new functionalities. This article reviews the current status of the field, concentrating on the first two, more mature research directions. From the fundamental point of view, (Ga,Mn)As and several other (III,Mn)V DMSs are now regarded as textbook examples of a rare class of robust ferromagnets with dilute magnetic moments coupled by delocalized charge carriers. Both local moments and itinerant holes are provided by Mn, which makes the systems particularly favorable for realizing this unusual ordered state. Advances in growth and postgrowth-treatment techniques have played a central role in the field, often pushing the limits of dilute Mn-moment densities and the uniformity and purity of materials far beyond those allowed by equilibrium thermodynamics. In (III,Mn)V compounds, material quality and magnetic properties are intimately connected. The present review focuses on the theoretical understanding of the origins of ferromagnetism and basic structural, magnetic, magnetotransport, and magneto-optical characteristics of simple (III,Mn)V epilayers, with the main emphasis on (Ga,Mn)As. Conclusions are arrived at based on an extensive literature covering results of complementary ab initio and effective Hamiltonian computational techniques, and on comparisons between theory and experiment. The applicability of ferromagnetic semiconductors in microelectronic technologies requires increasing Curie temperatures from the current record of 173 K in (Ga,Mn)As epilayers to above room temperature. The issue of whether or not this is a realistic expectation for (III,Mn)V DMSs is a central question in the field and motivates many of the analyses presented in this review. |
Semiconductor physics and magnetism are established subfields of condensed-matter physics that continue to reveal a rich variety of unusual phenomena, often in new types of solid-state materials. The properties of semiconductors are extraordinarily sensitive to impurity atoms, defects, and charges on external gates. Magnetism is a collective electronic phenomenon with an ordered state that is often stable to exceptionally high temperatures. Magnetic order, when it is present, has a large impact on other material properties including transport and optical properties. In both semiconductor and magnetic cases, sophisticated and economically important technologies have been developed to exploit the unique electronic properties, mainly for information processing in the case of semiconductors and for information storage and retrieval in the case of magnetism.
The realization of materials that combine semiconducting behavior with robust magnetism has long been a dream of material physics. One strategy for creating systems that are simultaneously semiconducting and magnetic, initiated in the late 1970s Jaczynski et al. (1978); Gaj et al. (1978), is to introduce local moments into well-understood semiconductors. The result is a new class of materials now known as diluted magnetic semiconductors (DMSs). Over the past 15 years, building on a series of pioneering publications in the 1990s Munekata et al. (1989); Ohno et al. (1992); Munekata et al. (1993); Ohno et al. (1996b); Hayashi et al. (1997); Van Esch et al. (1997); Ohno (1998), it has been established that several (III,V) compound semiconductors become ferromagnetic when heavily doped with Mn, and that the ferromagnetic transition temperatures can be well above 100 K. In semiconductors like GaAs and InAs, Mn has been shown to act both as an acceptor and as a source of local moments. These (III,Mn)V materials are examples of ferromagnetic semiconductors, a phrase we reserve for magnetic systems in which ferromagnetism is due primarily to coupling between magnetic element moments that is mediated by conduction-band electrons or valence-band holes. This definition implies that, in ferromagnetic semiconductors, magnetic properties can be influenced by the same assortment of engineering variables that are available for other more conventional semiconductor electronic properties. In the best-understood arsenide DMSs, semiconductor valence-band carriers participate in the magnetic order. The materials require participation of valence-band holes for the formation of a ferromagnetic state. Efforts to increase their critical temperatures further run into incompletely understood fundamental limits on the ratio of the magnetic transition temperature to the Fermi temperature of the free-carrier systems and are also affected by the role of disorder in these heavily doped materials. The tension between achieving high Curie temperatures and the desire for low, and therefore gateable, carrier densities is among the major issues in the study of these materials.
In this article we review the considerable theoretical progress that has been made in understanding the very broad range of properties that occur in (III,Mn)V ferromagnetic semiconductor epilayers in different regimes of Mn content and defect density. The main focus of this article is on the extensively studied (Ga,Mn)As ferromagnetic semiconductor, but we also make frequent comments on other (III,Mn)V DMSs. Comparisons to experimental data are made throughout the article. In Section I we review progress that has been achieved in the effort to realize useful DMS materials for spintronics (or magnetoelectronics). In Section II we discuss the properties of dilute Mn atoms in a (III,V) crystal, and the various mechanisms that can couple the orientations of distinct moments and lead to ferromagnetism. In Section III we discuss several different strategies that can be used to elevate material modeling from a qualitative to a more quantitative level. Sections IV–VII address a variety of different characteristics of (III,Mn)V layers, including their structural, magnetic, magnetotransport, and magneto-optical properties. Finally, in Section VIII we discuss the ferromagnetic ordering physics in (III,Mn)V DMSs in the broad context of magnetic interactions in systems with coupled local and itinerant moments, and then extrapolate from (III,Mn)V materials to comment on the effort to find high-temperature ferromagnetism in other DMS materials. We conclude in Section IX with a brief summary.
To partially remedy omissions in the bibliography that originate from our incomplete coverage of this topic, we refer to an extended database of published work and preprints maintained at http://unix12.fzu.cz/ms. The structure of the database is similar to the structure of this review and we encourage the reader in need of a more detailed bibliography to use this resource.
A number of review articles on various aspects of the physics of DMSs have been published previously and may help the reader who seeks a broader scope than we are able to supply in this review. The extensive body of research on DMSs in the 1980s, focused mostly on (II,Mn)VI alloys, has been reviewed by Furdyna and Kossut (1988); Furdyna (1988), and Dietl (1994). Several extended papers cover the experimental properties of (III,Mn)V DMSs, particularly (Ga,Mn)As and (In,Mn)As, interpreted within the carrier-mediated ferromagnetism model Ohno (1999); Matsukura et al. (2002); MacDonald et al. (2005). Theoretical predictions based on this model for a number of properties of bulk DMSs and heterostructures have been reviewed by Dietl (2002); Lee et al. (2002); König et al. (2003), and Dietl (2003). A detailed description of wide-band-gap and oxide DMSs can be found in Pearton et al. (2003); Graf et al. (2003b); Fukumura et al. (2004, 2005); Liu et al. (2005). We also mention here several specialized theoretical reviews focusing on the predictions of density-functional first-principles calculations for (III,Mn)V DMSs Sanvito et al. (2002); Sato and Katayama-Yoshida (2002), on Mn-doped II-VI and III-V DMSs in the low-carrier-density regime Bhatt et al. (2002), and on effects of disorder in (Ga,Mn)As Timm (2003).
III-V materials are among the most widely used semiconductors. There is little doubt that ferromagnetism in these materials would enable a host of new microelectronics device applications if the following criteria were met: (i) the ferromagnetic transition temperature should safely exceed room temperature, (ii) the mobile charge carriers should respond strongly to changes in the ordered magnetic state, and (iii) the material should retain fundamental semiconductor characteristics, including sensitivity to doping and light, and electric fields produced by gate charges. For more than a decade these three key issues have been the focus of intense experimental and theoretical research into the material properties of Mn-doped III-V compounds. At first sight, fundamental obstacles appear to make the simultaneous achievement of these objectives unlikely. Nevertheless, interest in this quest remains high because of the surprising progress that has been achieved. Highlights of this scientific endeavor are briefly reviewed in this introductory section.
Under equilibrium growth conditions the incorporation of magnetic Mn ions into III-As semiconductor crystals is limited to approximately 0.1%. Beyond this doping level, surface segregation and phase separation occur. To circumvent the solubility problem a nonequilibrium, low-temperature molecular-beam-epitaxy (LT MBE) technique was applied and led to the first successful growth of (In,Mn)As and (Ga,Mn)As DMS ternary alloys with more than 1% Mn. Since the first report in 1992 of a ferromagnetic transition in p-type (In,Mn)As at a critical temperature Tc = 7.5 K Ohno et al. (1992), the story of critical temperature limits in (III,Mn)V DMSs has unfolded in different stages. Initial experiments in (In,Mn)As suggested an intimate relation between the ferromagnetic transition and carrier localization, reminiscent of the behavior of manganites (perovskite (La,A)MnO3 with A=Ca, Sr, or Ba) in which ferromagnetism arises from a Zener double-exchange process associated with d-electron hopping between Mn ions Coey et al. (1999). (We comment at greater depth on qualitative pictures of the ferromagnetic coupling in Sections 2.1 and 8.1.) This scenario was corroborated by a pioneering theoretical ab initio study of the (In,Mn)As ferromagnet Akai (1998) and the mechanism was also held responsible for mediating ferromagnetic Mn-Mn coupling in some of the first ferromagnetic (Ga,Mn)As samples with Tc’s close to 50 K Van Esch et al. (1997).
In 1998 the Tohoku University group announced a jump of Tc in p-type (Ga,Mn)As to 110 K Ohno (1998) and pointed out that the critical-temperature value was consistent with the kinetic-exchange mechanism for ferromagnetic coupling, also first proposed by Zener (see Section 2.1). In its simplest form, ferromagnetism in this picture follows Dietl et al. (1997) from Ruderman-Kittel-Kasuya-Yosida (RKKY) indirect coupling between Mn d-shell moments mediated by induced spin polarization in a free-hole itinerant-carrier system (see Sections 2.1, 5.1.2, and 8.1). Zener proposed this mechanism originally for transition-metal ferromagnets for which the applicability of this picture is now known to be doubtful because of the itinerant character of transition-metal d electrons. The model of Mn(d5) local moments that are exchange-coupled to itinerant sp-band carriers does, however, provide a good description of Mn-doped IV-VI and II-VI DMSs Dietl (1994). The key difference between (III,Mn)V materials like (Ga,Mn)As and IV-VI and II-VI DMSs is that Mn substituting for the trivalent cation (Ga) is simultaneously an acceptor and a source of magnetic moments. Theoretical critical-temperature calculations based on the kinetic-exchange model predict room-temperature ferromagnetism in (Ga,Mn)As with 10% Mn content. In spite of these optimistic predictions, the goal of breaking the 110 K record in (Ga,Mn)As remained elusive for nearly four years. Only recently has progress in MBE growth and in the development of post growth annealing techniques Hayashi et al. (2001); Yu et al. (2002); Edmonds et al. (2002a); Chiba et al. (2003a); Ku et al. (2003); Eid et al. (2005) made it possible to suppress extrinsic effects, pushing Tc in (Ga,Mn)As up to 173 K Wang et al. (2005a); Jungwirth et al. (2005b). Tc trends in current high quality (Ga,Mn)As epilayers are consistent with the Zener kinetic-exchange model Jungwirth et al. (2005b). The current Tc record should be broken if DMS material with a higher concentration of substitutional Mn ions can be grown.
Based on the few experimental and theoretical studies reported to date, (III,Mn)Sb DMSs are expected to fall into the same category as (Ga,Mn)As and (In,Mn)As DMSs. The kinetic-exchange model calculations predict Tc’s that are small compared to their arsenide counterparts Dietl et al. (2000); Jungwirth et al. (2002b). This difference, confirmed by experiment Abe et al. (2000); Wojtowicz et al. (2003); Panguluri et al. (2004); Csontos et al. (2005), is caused by the weaker p-d exchange and smaller magnetic susceptibility (smaller effective mass) of itinerant holes in the larger-unit-cell antimonides. Also consistent with the kinetic-exchange model is the remarkable observation of an increase of Tc in (In,Mn)Sb by 25% induced by the applied hydrostatic pressure Csontos et al. (2005).
Moving in the opposite direction in the periodic table toward (III,Mn)P and (III,Mn)N appears to be the natural route to high-Tc ferromagnetic semiconductors. The kinetic-exchange model predicts Tc’s far above room temperature in these smaller-lattice-constant materials, in particular, in (Ga,Mn)N Dietl et al. (2000). Also, the solubility limit of Mn is much larger than in arsenides, making it possible in principle to grow highly-Mn-doped DMSs under or close to equilibrium conditions. However, the nature of magnetic interactions in Mn-doped phosphides and nitrides is not completely understood either theoretically or experimentally Liu et al. (2005). As the valence-band edge moves closer to the Mn d level and the p-d hybridization increases with increasing semiconductor gap width and decreasing lattice constant, charge fluctuations of d states may become large Sanyal et al. (2003); Wierzbowska et al. (2004); Sandratskii et al. (2004). With increasing ionicity of the host crystal, the Mn impurity may also undergo a transition from a d5 divalent acceptor to a d4 trivalent neutral impurity Luo and Martin (2005); Kreissl et al. (1996); Schulthess et al. (2005). In either case, the picture of ferromagnetism based on the Zener kinetic-exchange model needs to be reconsidered in these materials.
Experimental critical temperatures close to 1000 K have been reported in some (Ga,Mn)N samples Sasaki et al. (2002a). It is still unclear, however, whether the high-temperature ferromagnetic phase should be attributed to a (Ga,Mn)N ternary alloy or to the presence of ferromagnetic metal precipitates embedded in the host GaN lattice. Reports of (Ga,Mn)N epilayers synthesized in cubic and hexagonal crystal structures, of p-type and n-type ferromagnetic (Ga,Mn)N, and of multiple ferromagnetic phases in one material all add to the complex phenomenology of these wide-gap DMSs Korotkov et al. (2001); Graf et al. (2002, 2003a); Arkun et al. (2004); Edmonds et al. (2004c); Hwang et al. (2005); Edmonds et al. (2005b); Sawicki et al. (2005a).
Uncertainties apply also to the interpretation of ferromagnetism seen in the (Ga,Mn)P samples studied to date, which have been prepared by post-MBE ion implantation of Mn followed by rapid thermal Theodoropoulou et al. (2002); Poddar et al. (2005) or pulse-laser-melting annealing Scarpulla et al. (2005). Experiments in these materials have not yet established unambiguously the nature of magnetic interactions in the (III,Mn)P compounds. However, a comparative study of (Ga,Mn)P and (Ga,Mn)As prepared by the post-MBE ion implantation and pulse-laser-melting annealing suggests carrier-mediated origin of ferromagnetism in the (Ga,Mn)P material Scarpulla et al. (2005).
Our current understanding of the material physics of (III,Mn)V DMS epilayers suggests that synthesis of a room-temperature ferromagnetic semiconductor will require a level of doping and defect control comparable to what has now been achieved in high-quality (Ga,Mn)As samples, Mn densities of order 10%, and may require the use of wider-gap III-V alloys.
Finally, we note that efforts to enhance the Curie temperature in Mn-doped (III,V) semiconductors have also led to material research in more complex semiconductor heterostructures with highly Mn-doped monolayers (δ-doped layers), showing promising results Nazmul et al. (2005); Kawakami et al. (2000); Chen et al. (2002); Fernández-Rossier and Sham (2002); Nazmul et al. (2003); Sanvito (2003); Myers et al. (2004); Vurgaftman and Meyer (2001).
Spintronic devices exploit the electron spin to manipulate the flow of electrons and therefore require materials in which the charge and spin degrees of freedom of carriers are strongly coupled Wolf et al. (2001); De Boeck et al. (2002); Zutic et al. (2004). The most robust, and currently the most useful, spintronic devices rely on the collective behavior of many spins in ferromagnetic materials to amplify the coupling of external magnetic fields to electronic spins, a coupling that is very weak for individual electrons. The intrinsically large spin-orbit interaction in III-Sb and III-As valence-band states makes these hosts ideal candidates for exploring various spintronic functionalities. In (Ga,Mn)As DMS epilayers, for example, the measured anisotropic magnetoresistance (AMR) effect (the relative difference between longitudinal resistivities for different magnetization orientations) can reach ~ 10% Wang et al. (2002); Baxter et al. (2002); Jungwirth et al. (2002a); Tang et al. (2003); Jungwirth et al. (2003b); Matsukura et al. (2004); Wang et al. (2005c); Goennenwein et al. (2005).
A particularly strong manifestation of valence-band spin-orbit coupling occurs in the antisymmetric off-diagonal element of the resistivity tensor. The anomalous Hall effect (AHE) shown in Fig. 1, which completely dominates the low-field Hall response in (Ga,Mn)As and some other III-V DMSs, has become one of the key tools used to detect the paramagnetic/ferromagnetic transition Ohno et al. (1992); Ohno (1998). Its large value is due to the spin-polarization of holes and provides strong evidence for the participation of mobile charge carriers in the ordered magnetic state of these DMSs.
|
|
In metals, the current response to changes in the magnetic state is strongly enhanced in layered structures consisting of alternating ferromagnetic and nonmagnetic materials. The giant-magnetoresistance effect Baibich et al. (1988), which is widely exploited in current technology, for example, in field sensors and magnetic random-access memories, reflects the large difference between resistivities in configurations with parallel and antiparallel polarizations of ferromagnetic layers in magnetic superlattices or trilayers like spin valves and magnetic tunnel junctions Gregg et al. (2002). The effect relies on transporting spin information between layers and therefore is sensitive to spin-coherence times in the system. Despite strong spin-orbit coupling, which reduces spin coherence in DMSs, functional spintronic trilayer devices can be built, as demonstrated by the measured large MR effects in (Ga,Mn)As-based tunneling structures Tanaka and Higo (2001); Chiba et al. (2004a); Saito et al. (2005); Mattana et al. (2005). The coercivities of individual DMS layers can be tuned via exchange biasing to an antiferromagnet Eid et al. (2004) which is a standard technique used in metal giant-magnetoresistance devices Gregg et al. (2002).
DMS ferromagnets possess all properties that are exploited in conventional spintronics. They qualify as ferromagnetic semiconductors to the extent that their magnetic and other properties can be altered by usual semiconductor electronics engineering variables. The achievement of ferromagnetism in an ordinary III-V semiconductor that includes several percent of Mn demonstrates on its own the sensitivity of magnetic properties to doping. Remarkably, doping profiles and, correspondingly, magnetic properties can be grossly changed, even after growth, by annealing. Early studies of (Ga,Mn)As indicated that annealing at temperatures above the growth temperature leads to a reduction of magnetically and electrically active Mn ions and, at high enough annealing temperatures, to the formation of MnAs clusters Van Esch et al. (1997). On the other hand, annealing at temperatures below the growth temperature can substantially improve magnetic and transport properties of the thin DMS layers due to the out-diffusion of charge- and moment-compensating defects, now identified as interstitial Mn Yu et al. (2002); Edmonds et al. (2002a); Chiba et al. (2003a); Ku et al. (2003); Eid et al. (2005).
(In,Mn)As-based field-effect transistors were built to study electric field control of ferromagnetism in DMSs. It has been demonstrated that changes in the carrier density and distribution in thin-film DMS systems due to an applied bias voltage can reversibly induce the ferromagnetic/paramagnetic transition Ohno et al. (2000). Another remarkable effect observed in this magnetic transistor is electric-field-assisted magnetization reversal Chiba et al. (2003b). This novel functionality is based on the dependence of the hysteresis loop width on bias voltage, again through the modified charge-density profile in the ferromagnetic semiconductor thin film.
|
|
Experiments in which ferromagnetism in a (III,Mn)V DMS system is turned on and off optically add to the list of functionalities that result from the realization of carrier-induced ferromagnetism in a semiconductor host material Munekata et al. (1997); Koshihara et al. (1997). The observed emission of circularly polarized light from a semiconductor heterostructure, in which electrons (holes) injected from one side of the structure recombine with spin-polarized holes (electrons) emitted from a DMS layer Fiederling et al. (1999); Ohno et al. (1999), is an example of phenomena that may lead to novel magneto-optics applications.
Tunneling anisotropic magnetoresistance (TAMR) is another novel spintronic effect observed in (Ga,Mn)As Gould et al. (2004); Brey et al. (2004); Rüster et al. (2005); Saito et al. (2005). TAMR, like AMR, arises from spin-orbit coupling and reflects the dependence of the tunneling density of states of the ferromagnetic layer on the orientation of the magnetization with respect to the current direction or crystallographic axes.
The larger characteristic electronic length scales in DMSs compared to ferromagnetic metals make it possible to lithographically define lateral structures with independent magnetic areas coupled through depleted regions that act as tunnel barriers and magnetic weak links. The electrical response to magnetization reversals in these spintronic nanodevices can lead to MR effects with magnitudes of order 1000% Rüster et al. (2003), as shown in Fig. 2, and with a rich phenomenology Giddings et al. (2005). Wider lateral constrictions have been used to demonstrate controlled domain-wall nucleation and propagation in DMS stripes Rüster et al. (2003); Honolka et al. (2005), a prerequisite for developing semiconductor logic gates based on magnetic domain manipulation Gate and Register (2002); Allwood et al. (2005). (Ga,Mn)As nanoconstrictions with lateral side gates have revealed a new effect, Coulomb blockade anisotropic magnetoresistance, which reflects the magnetization orientation dependence of the single-electron charging energy Wunderlich et al. (2006). These spintronic single-electron transistors offer a route to nonvolatile, low-field, and highly electrosensitive and magnetosensitive operation.
The magnetic dipole-dipole interaction strength between two discrete moments separated by a lattice constant in a typical solid is only ~ 1 K, relegating direct magnetic interactions to a minor role in the physics of condensed-matter magnetic order. Relativistic effects that lead to spin-orbit coupling terms in the Hamiltonian provide a more plausible source of phenomena that are potentially useful for spintronics. Although these terms are critical for specific properties like magnetic anisotropy, they are rarely, if ever, crucial for the onset of the magnetic order itself. Instead the universal ultimate origin of ferromagnetism is almost always the interplay between the electronic spin degree of freedom, the repulsive Coulomb interactions between electrons, and the fermionic quantum statistics of electrons. The Pauli exclusion principle correlates the spin and orbital parts of the many-electron wave function by requiring the total wave function to be antisymmetric under particle exchange. Whenever groups of electrons share the same spin state, the orbital part of the many-body wave function is locally antisymmetric, lowering the probability of finding electrons close together and hence the interaction energy of the system. Because magnetic order is associated with the strong repulsive Coulomb interactions between electrons, it can persist to very high temperatures, often to temperatures comparable to those at which crystalline order occurs. Ferromagnetism can be as strong as chemical bonds. Very often the quantum ground state of a many-electron system has nonzero local spin density, aligned either in the same direction in space at every point in the system as in simple ferromagnets, or in noncollinear, ferrimagnetic, or antiferromagnetic materials in configurations in which the spin direction varies spatially.
Although this statement on the origin of magnetic order has very general validity, its consequences for a system of nuclei with a particular spatial arrangement, are extraordinarily difficult to judge. Because ferromagnetism is a strong-coupling phenomenon, rigorous theoretical analyses are usually not possible. There is no useful universal theory of magnetism. Understanding magnetic order in a particular system or class of systems can be among the most challenging of solid state physics problems Ashcroft and Mermin (1976); Marder (1999). For most systems, it is necessary to proceed in a partially phenomenological way, by identifying the local spins that order, and determining the magnitude and sign of the exchange interactions that couple them by comparing the properties of simplified (often ‘spin-only’) model Hamiltonians with experimental observations.
One approach that is totally free of phenomenological parameters is density-functional theory (DFT), including its spin-density-functional (SDF) generalizations in which energy functionals depend on charge and spin densities. Although DFT theory is exact in principle, its application requires that the formalism’s exchange-correlation energy functional be approximated. Approximate forms for this functional can be partially phenomenological (making a pragmatic retreat from the ab initio aspiration of this approach) and are normally based in part on microscopic calculations of correlation effects in the electron-gas model system. This is the case for the often-used local-(spin-)density approximation (L(S)DA) von Barth and Hedin (1972). For many magnetic metals, in which correlations are somewhat similar to those in the electron-gas model system, ab initio LSDA theory provides a practical and sufficiently accurate solution of the magnetic many-body problem Jones and Gunnarsson (1989). This is particularly true for the elemental transition-metal ferromagnets Fe, Co, and Ni and their alloys Moruzzi and Marcus (1993); Marder (1999). In practice LSDA theory functions as a mean-field theory in which the exchange energy at each point in space increases with the self-consistently determined local spin density. With increasing computer power, LSDA theory has been applied to more complex materials, including DMSs.
As we discuss below, both phenomenological and DFT approaches provide valuable insight into (III,Mn)V ferromagnetism. Model Hamiltonian theories are likely to remain indispensable because, when applicable, they provide more transparent physical pictures of ferromagnetism and often enable predictions of thermodynamic, transport, and other properties that are sometimes (depending on material complexity), beyond the reach of ab initio theory techniques. Of particular importance for DMSs is the capability of model Hamiltonians to describe localized electronic levels coincident with an itinerant-electron band which, strictly speaking, is beyond the reach of the effectively one-particle band theories of solids that emerge from LSDA theory Anderson (1961); Schrieffer and Wolff (1966). Interpreting experiments with model Hamiltonian approaches can, on the other hand, be misleading if the model is too simplified and important aspects of the physics are absent from the model. What is more, even simplified models usually leave complex many-body problems that cannot be completely solved.
Magnetism in (Ga,Mn)As and some other (III,Mn)V ferromagnets originates from Mn local moments. (As already pointed out, Mn-doped phosphides and nitrides DMSs are less well understood; however, local Mn moments are likely to play an important role in these materials as well.) The dependence of the energy of the system on the relative orientation of Mn moments is generally referred to as an exchange interaction. This terminology is part of the ‘jargon’ of magnetism and recognizes that Fermi statistics is the ultimate origin. Several types of qualitative effect that lead to exchange interactions can be separately identified when addressing magnetic order in (III,Mn)V DMSs; the applicability of each and the relative importance of different effects may depend on the doping regime and on the host semiconductor material. In this section we first introduce the terminology that is commonly used in the magnetism literature, by briefly reviewing some of the effects that can lead to magnetic coupling, most of which have been recognized since near the dawn of quantum mechanics.
For spins carried by itinerant electrons, exchange interactions are often most simply viewed from a momentum space rather than a real-space point of view. Stoner’s itinerant exchange Ashcroft and Mermin (1976) favors spontaneous spin polarization of the entire electron gas because electrons are less likely to be close together and have strongly repulsive interactions when they are more likely to have the same spin. Because the band energy is minimized by double occupation of each Bloch state, the Stoner ferromagnetic instability occurs in systems with a large density of states at the Fermi energy. This helps to explain, for example, why ferromagnetism occurs in the late 3d transition elements. A large density of states makes it possible to gain exchange energy by moving electrons from one spin band to the other while keeping the kinetic-energy cost sufficiently low. Since the key spins in many (III,Mn)V DMS materials are localized the Stoner mechanism does not drive ferromagnetism, although we will see in Section 5.1 that it still plays a minor supporting role.
In many systems, including (III,Mn)V DMSs, both the local nature of the moments and strong local Coulomb interactions that suppress charge (valence) fluctuations play a key role and have to be included even in a minimal model. Many mechanisms have been identified that couple localized spins in a solid. The origin of Heisenberg’s direct exchange Ashcroft and Mermin (1976) between two local spins is the difference between the Coulomb energy of a symmetric orbital wave function (antisymmetric singlet spin wave function) state and an antisymmetric orbital wavefunction (symmetric triplet spin wavefunction) state. Kramer’s superexchange interaction Anderson (1950), applies to local moments that are separated by a nonmagnetic atom. In a crystal environment, an electron can be transferred from the nonmagnetic atom to an empty shell of the magnetic atom and interact, via direct exchange, with electrons forming its local moment. The nonmagnetic atom is polarized and is coupled via direct exchange with all its magnetic neighbors. Whether the resulting superexchange interaction between local moments is ferromagnetic or antiferromagnetic depends on the relative sign of the two direct-exchange interactions Goodenough (1958); Kanamori (1959). In (III,Mn)V materials, superexchange gives an antiferromagnetic contribution to the interaction between Mn moments located on neighboring cation sites.
Zener’s double-exchange mechanism Zener (1951b) also assumes an intermediate nonmagnetic atom. In its usual form, this interaction occurs when the two isolated magnetic atoms have a different number of electrons in the magnetic shell and hopping through the intermediate nonmagnetic atom involves magnetic-shell electrons. Combined with the on-shell Hund’s rule, double exchange couples magnetic moments ferromagnetically. Parallel spin alignment is favored because it increases the hopping probability and therefore decreases the kinetic energy of spin-polarized electrons. A version of double exchange, in which Mn acceptor states form an impurity band with mixed spd character, has often been referred to in the (III,Mn)V literature. In this picture electrical conduction and Mn-Mn exchange coupling are both realized through hopping within an impurity band. The potential importance of double exchange is greater at lower Mn doping and in wider-gap (III,Mn)V materials.
Finally, we identify Zener’s kinetic-exchange Zener (1951a) or indirect-exchange interaction. It arises in models with local, usually d-shell or f-shell, moments whose coupling is mediated by s- or p-band itinerant carriers. The local moments can have a ferromagnetic direct-exchange interaction with band electrons on the same site and/or an antiferromagnetic interaction due to hybridization between the local moment and band electrons on neighboring sites Bhattacharjee et al. (1983); Dietl (1994). Polarization of band electrons due to the interaction at one site is propagated to neighboring sites. When the coupling is weak (the band carrier polarization is weak, e.g., at temperatures near the Curie temperature), the effect is described by RKKY theory, which was originally applied to carrier-mediated indirect coupling between nuclear moments Fröhlich and Nabarro (1940); Ruderman and Kittel (1954); Bloembergen and Rowland (1955); Yosida (1957) and between local d-shell moments in metals Zener (1951a); Kasuya (1956); Yosida (1957). The range of this interaction can be long and interactions between separate local moments can be either ferromagnetic or antiferromagnetic and tend to vary in space on the length scale of the itinerant band’s Fermi wavelength. Unlike the double-exchange case, magnetic order in this case does not lead to a significant change in the width of the conducting band. This type of mechanism certainly does play a role in (III,Mn)V ferromagnetism, likely dominating in the case of strongly metallic (Ga,Mn)As, (In,Mn)As, and Mn-doped antimonides. There is no sharp distinction between impurity-band double-exchange and kinetic-exchange interactions; the former is simply a strong-coupling, narrow-band limit of the latter.
The starting point for developing a useful predictive model of (III,Mn)V ferromagnetism is achieving a full understanding of the electronic state with a single Mn impurity in the host lattice. We need to fully understand the character of the isolated local moments before we can critically discuss how they are coupled. The character of the local moment need not be the same in all (III,Mn)V materials. The remaining subsections will focus on properties of a Mn impurity in GaAs and on the nature of ferromagnetic coupling in (Ga,Mn)As and related arsenide and antimonide DMSs. At the end of this section, we comment on how things might change in wider-gap hosts like GaP and GaN.
Among all (III,V) hosts, Mn impurity has been studied most extensively in GaAs. The elements in the (Ga,Mn)As compound have nominal atomic structures [Ar]3d104s2p1 for Ga, [Ar]3d54s2 for Mn, and [Ar]3d104s2p3 for As. This circumstance correctly suggests that the most stable and therefore most common position of Mn in the GaAs host lattice is on the Ga site where its two 4s electrons can participate in crystal bonding in much the same way as the two Ga 4s electrons. The substitutional MnGa, and the less common interstitial MnI, positions are illustrated in Fig. 3. Because of the missing valence 4p electron, the MnGa impurity acts as an acceptor. In the electrically neutral state, labeled as A0(d5 + hole), Mn Ga has the character of a local moment with zero angular momentum and spin S = 5∕2 (Landé g factor g = 2) and a moderately bound hole. The local moment is formed by three occupied sp-d bonding states with dominant t2g (3dxy, 3dxz, 3dyz) character and by two occupied eg (3dx2-y2, 3dz2) orbitals that are split from the t2g states by the tetrahedral crystal field and do not strongly hybridize with the sp orbitals. All occupied d orbitals have the same spin orientation and together comprise the S = 5∕2 local moment. The weakly bound hole occupies one of the three antibonding sp-d levels with dominant As 4p character. The charge -e ionized MnGa acceptor center, labeled as A-(d5), has just the S = 5∕2 local spin character.
|
|
Electron paramagnetic resonance (EPR) and ferromagnetic resonance (FMR) experiments confirm the presence of the A-(d5) center through the entire range of Mn concentrations in both bulk and epilayer (Ga,Mn)As Almeleh and Goldstein (1962); Szczytko et al. (1999b); Sasaki et al. (2002b). The S = 5∕2 local moment on Mn was detected through a resonance line centered at g = 2 and, in low-Mn-density samples, through a sextet splitting of the line due to the hyperfine interaction with the I = 5∕2 55Mn nuclear spin. The neutral MnGa centers are more elusive because of nearly full compensation by unintentional donor impurities at low Mn concentrations and because of the metal-insulator transition at high Mn concentrations. Nevertheless, a multitude of experimental techniques, including EPR Schneider et al. (1987), infrared (IR) spectroscopy Chapman and Hutchinson (1967); Linnarsson et al. (1997), and magnetization measurements Frey et al. (1988), have detected the A0(d5 + textrmhole) center in (Ga,Mn)As. Strikingly direct evidence was given by an STM experiment Yakunin et al. (2004b,a); Kitchen et al. (2005), shown in Fig. 4, in which the state of a single impurity atom was switched between the ionized A-(d5) and neutral A0(d5 + hole) states by applying a bias voltage that corresponded to a binding energy Eb ≈ 0.1 eV.
|
|
The binding energy Eb = 112.4 meV inferred from IR spectroscopy Linnarsson et al. (1997); Chapman and Hutchinson (1967) is consistent with the above STM measurement and with inferences based on photoluminescence experiments Lee and Anderson (1964); Schairer and Schmidt (1974). These observations identify Mn as a moderately shallow acceptor in GaAs whose band gap is Eg = 1.52 eV. The binding energy, which governs the electrical behavior of the Mn impurity, has contributions from both Coulomb attraction between the hole and the A-(d5) core (and a central cell correction) and spin-dependent p-d hybridization. The latter effect is responsible for the exchange interaction on which this review centers. We now discuss this parameter in more detail.
The top of the GaAs valence band is dominated by 4p levels which are more heavily weighted on As than on Ga sites. Direct exchange between holes near the top of the band and localized Mn d electrons is weak since MnGa and As belong to different sublattices. This fact allows p-d hybridization to dominate, explaining the antiferromagnetic sign of this interaction Bhattacharjee et al. (1983) seen in experiment Okabayashi et al. (1998).
There is a simple physical picture of the p-d exchange interaction which applies when interactions are treated in a mean-field way, and therefore also applies as an interpretation of LSDA calculations. Given that the filled, say spin-down, Mn d-shell level is deep in the valence band and that the empty spin-up d level is above the Fermi level and high in the conduction band, hybridization (level repulsion of like-spin states) pushes the energy of spin-down valence-band states up relative to the energy of spin-up valence-band states. The resulting antiferromagnetic coupling between valence-band states and local Mn spins is illustrated schematically in Fig. 5. The same basic picture applies for itinerant valence-band states in a heavily doped metallic DMS and for the acceptor state of an isolated MnGa impurity. Note that the cartoon band structure in Fig. 5 is plotted in the electron picture while the DMS literature usually refers to the antiferromagnetic p-d coupling between holes and local Mn moments. We comment in detail on the equivalent notions of p-d exchange in the physically direct electron picture and the computationally more convenient hole picture for these p-type DMSs in Section 5.2.
|
|
We have already mentioned in Section 2.1 the conceptional inadequacy of effective single-particle theories, including the LSDA, in dealing with local moment levels coincident with itinerant-electron bands. Anderson suggested a many-body model Hamiltonian that circumvents this problem by including explicitly the Coulomb correlation integral of localized electron states in the Hamiltonian Anderson (1961); Haldane and Anderson (1976); Fleurov and Kikoin (1976). The problem is that the change in the effective potential when the number of occupied localized orbitals changes by one, the Hubbard constant U, can be comparable to or larger than other band parameters, invalidating any mean-field-like approach. The consequences of this fact can be captured at a qualitative level in models that include the Hubbard U Krstajić et al. (2004). In these phenomenological models, the localized orbital part of the Hamiltonian generally has an additional parameter, the Hund’s rule constant JH. This parameter captures the local direct-exchange physics, which favors spin-polarized open-shell atomic states. For the case of the Mn(d5) configuration, JH forces all five singly occupied d orbitals to align their spins in the ground state. Recently, considerable effort has been devoted to developing approaches that combine the local correlation effects induced by the U and JH terms in phenomenological models, with SDF theory Anisimov et al. (1991); Perdew and Zunger (1981); Park et al. (2000); Sandratskii et al. (2004); Petit et al. (2006); Wierzbowska et al. (2004); Filippetti et al. (2005); Schulthess et al. (2005). We comment on these ab initio techniques in Section 3.1.
When hybridization Slater and Koster (1954); Harrison (1980) between the local-moment and band-electron states is weak it can be treated perturbatively. The Schrieffer-Wolff transformation of the Anderson Hamiltonian,
removes the hybridization (the last term in Eq. (1) and leads to a model in which the local-moment spin interacts with the valence band via a spin-spin interaction only, ∑ k′kjk′ksd ⋅ sk′k, with the number of electrons in each band fixed Schrieffer and Wolff (1966). Here we assume for simplicity a single localized orbital and a single itinerant band, and use k to represent band states and d to represent the localized impurity state, s labels spin, εα is the single particle energy, and nα = cα†c α and cα are standard second quantization operators. This procedure is normally useful only if the hybridization is relatively weak, in which case it is not usually a problem to forget that the canonical transformation should also be applied to operators representing observables. Strictly speaking, the Schrieffer-Wolff transformation also leads to a spin-independent interaction Schrieffer and Wolff (1966) which is normally neglected in comparison with the stronger spin-independent long-range part of the Coulomb potential.Since valence-band states of interest in GaAs, even in heavily doped samples, are near the Brillouin-zone center Γ, the single phenomenological constant extracted from experiment for this interaction should be thought of as its value when both initial and final states are at the Γ point. The quantity ∑ k′kjk′ksdsk′k is then approximated by J0sd ⋅ sk=0, where
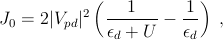 | (2) |
V pd represents the As p-orbital–Mn d-orbital hybridization potential (neglecting again the multiple-orbital nature of p and d levels for simplicity), εd < 0 is the single-particle atomic-level energy of the occupied Mn d state measured from the top of the valence band, and εd + U > 0 is the energy cost of adding a second electron to this orbital Schrieffer and Wolff (1966). When the hole density is large or holes are more strongly localized near Mn acceptors, the crystal-momentum dependence of this interaction parameter cannot be entirely neglected Timm and MacDonald (2005).
Since J0 originates from hopping between Mn and neighboring As atoms, the p-d exchange potential J(Ri -r) produced by Mn impurity at site Ri has a range of order one lattice constant, and
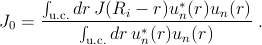 | (3) |
In Eq. (3) we assumed that the perfect-crystal Bloch function, ψn,k(r) = exp(ikr)un,k(r), is composed of a slowly varying envelope function and a periodic function un,k(r) with the normalizations 1∕V ∫ dr ψn,k*(r)ψ n′,k′(r) = δn,n′δk,k′ and 1∕Ωu.c. ∫ u.c.dr un*(r)u n′(r) = δn,n′. Here V is the crystal volume and Ωu.c. is the unit-cell volume. In GaAs, Ωu.c. = alc3∕4=0.045 nm3 and the lattice constant alc = 0.565 nm. These wave functions can be obtained from k ⋅ p theory which treats the band Hamiltonian of the system perturbatively, expanding around the Γ point Dietl et al. (2001b); Abolfath et al. (2001a). J0 in Eq. (3) corresponds to the average value of J(Ri - r) experienced by the k = 0 Bloch state over the ith unit cell.
The slowly varying envelope function experiences an effective zero-range p-d exchange potential, since
![〈ψn,k∣J(Ri - r)∣ψn′,k′〉
-1 ∫ ′ *
= V dr exp [i(k - k )r]J(Ri - r)u n,k(r)un′,k′(r)
Nu.c. ∫
≈ -1 ∑ exp [i(k - k′)Rj] dr J(Ri - r)u* (r)un(r)
V j=1 j-u.c. n
Nu.c.
-1 ∑ ′
= V exp [i(k - k )Rj]J0Ωu.c.δi,j
j∫=1
≈ -1 dr exp [i(k - k′)r]J δ(R - r) , (4)
V pd i](review/auximages/review3x.png)
The value of the Jpd constant is often considered to be independent of the host semiconductor Dietl et al. (2000, 2001b); Jungwirth et al. (2002b). Indeed, the increase of ∣V pd∣2 ~ a lc-7 Harrison (1980) in Eq. (2) with decreasing lattice constant is partly compensated by smaller Ωu.c. (~ alc3), and the increase of ∣1∕εd∣ in a wider-gap host is partly compensated by the decrease of the term 1∕(εd + U). Although it may have similar values in many materials, Jpd will tend to be larger in larger-gap, smaller-lattice-constant hosts.
In a virtual-crystal mean-field approximation, the p-d exchange potential due to the Mn impurities in a Ga1-xMnxAs DMS, xN0Ωu.c. ∑ Ru.c.J(Ru.c. - r)〈S〉⋅ s, has the periodicity of the host crystal. (Here 〈S〉 is the mean-field Mn spin.) The valence-band states in this approximation experience an effective single-particle kinetic-exchange field, hMF = NMnJpd〈S〉, where NMn = xN0 is the MnGa density.
Finally, we discuss the relationship between the exchange constant Jpd and exchange constant, ɛ, used to provide a k ⋅p interpretation of spectroscopic studies of the neutral A0(d5 + hole) center. We emphasize that the use of a k ⋅p approach assumes that the bound hole is spread over at least several lattice constants in each direction. The fact that it is possible to achieve a reasonably consistent interpretation of detailed spectroscopic data in this way is in itself strong support for the validity of this assumption. Coupling between the weakly bound hole moment J and the local spin S of the MnGa core is expressed as ɛS ⋅ J, where J = j + L, j is the (atomic scale) total angular momentum operator of the band hole at the Γ point (j = 3∕2 or 1/2 for the As 4p orbitals forming the band states near k = 0), and L is the additional (hole binding radius scale) angular momentum acquired by the hole upon binding to the MnGa impurity. The IR spectroscopy data Linnarsson et al. (1997) have been analyzed Bhattacharjee and ŕ la Guillaume (2000) within a spherical approximation, i.e., considering only the L = 0, s-like bound state. (Note that a sizable anisotropic d-like component in the bound-hole ground state has been identified in the analysis of the STM data Tang and Flatté (2004); Yakunin et al. (2004b).) Further simplification is achieved by neglecting the admixture of the two j = 1∕2 (jz = ±1∕2) Γ-point states which is justified by the large spin-orbit splitting ΔSO = 341 meV of these states from two heavy-hole states (j = 3∕2, jz = ±3∕2) and two light-hole states (j = 3∕2, jz = ±1∕2).
Writing the ground-state wave function as ψjz(r) = Fjz(r)ujz(r) with a spherically symmetric envelope function Fjz(r) and for jz = ±3∕2,±1∕2 (j = 3∕2), the expectation value of the exchange potential reads
where ∣f(RI)∣2 = 〈F jz*(r)F jz(r)〉u.c. is the mean value of the slowly varying envelope function squared within the unit cell containing the MnGa impurity. Equation (5) implies that
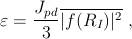 | (6) |
i.e., the ratio between ɛ and Jpd is determined by the strength of the hole binding to the A-(d5) Mn Ga core and is larger for more localized holes.
A combination of IR data and theoretical calculations has been used to analyze this in more detail Linnarsson et al. (1997); Bhattacharjee and ŕ la Guillaume (2000). First of all, the value of the g factor g = 2.77 of the neutral A0(d5 + hole) Mn Ga complex obtained from IR spectroscopy measurements is in agreement with the theoretical value expected for the total angular momentum state F = S - J = 1 of the complex, confirming the antiferromagnetic character of the p-d coupling between the hole and the local Mn spin. The contribution of the p-d potential to the binding energy is then given by ɛS ⋅ J = ɛ[F(F + 1) - S(S + 1) - J(J + 1)]∕2, which for the F = 1 ground state gives -21ɛ∕4. The IR spectroscopy measurement of the splitting 2ɛ between the F = 1 and F = 2 states gives ɛ ≈ 5 meV, i.e., the contribution to the binding energy from the p-d interaction is approximately 26.25 meV. The remaining binding energy, 112.4 - 26.25 = 86.15 meV, is due to the central field potential of the impurity. Bhattacharjee and Benoit Bhattacharjee and ŕ la Guillaume (2000) used the hydrogenic-impurity model with a screened Coulomb potential and a central cell correction, whose strength was tuned to reproduce the value 86.15 meV, to obtain a theoretical estimate for ∣f(RI)∣2 ≈ 0.35 nm-3. From Eq. (6) they obtained J pd ≈ 40 meV nm3. Given the level of approximation used in the theoretical description of the A0(d5 + hole) state, this value is in a reasonably good agreement with the exchange constant value Jpd = 54 ± 9 meV nm3 (N 0β = 1.2 ± 0.2 eV) inferred from photoemission data Okabayashi et al. (1998). We note here that photoemission spectroscopy Okabayashi et al. (1998, 1999, 2001, 2002); Rader et al. (2004); Hwang et al. (2005) has represented one of the key experimental tools to study the properties of Mn impurities in DMSs, in particular, the position of the Mn d level and the strength and sign of the p-d coupling. An indirect measurement of the Jpd constant is performed by fitting the photoemission data to a theoretical spectrum of an isolated MnAs4 cluster Okabayashi et al. (1998). This procedure is justified by the short-range character of the p-d exchange interaction.
Most of the single-Mn-impurity spectroscopic studies mentioned above were performed in samples with doping levels x < 0.1% for which the Ga1-xMnxAs random alloy can be grown under equilibrium conditions. In these materials Mn can be expected to occupy almost exclusively the low-energy Ga-substitutional position. Ferromagnetism, however, is observed only for x > 1% which is well above the equilibrium Mn solubility limit in GaAs and therefore requires a nonequilibrium growth technique (in practice low-temperature MBE) to avoid Mn precipitation. The price paid for this is the occurrence of a large number of metastable impurity states. The most important additional defects are interstitial Mn ions and As atoms on cation sites (antisite defects). Both act as donors and can have a severe impact on the electric and magnetic properties of DMS epilayers. More unintended defects form at higher Mn doping because of the tendency of the material, even under nonequilibrium growth conditions, toward self-compensation.
Direct experimental evidence for Mn impurities occupying interstitial (MnI) rather than substitutional positions was uncovered by combined channeling Rutherford backscattering and particle-induced x-ray emission measurements Yu et al. (2002). This technique can distinguish between MnI and MnGa by counting the relative numbers of exposed Mn atoms and the ones shadowed by lattice-site host atoms at different channeling angles. In highly doped as-grown samples, the experiment identified nearly 20% of Mn as residing on interstitial positions. The metastable nature of these impurities is manifested by the substantial decrease in their density upon postgrowth annealing at temperatures very close to the growth temperatures Yu et al. (2002); Edmonds et al. (2002a); Chiba et al. (2003a); Ku et al. (2003); Stone et al. (2003). Detailed resistance-monitored annealing studies combined with Auger surface analysis established the out-diffusion of MnI impurities toward the free DMS epilayer surface during annealing Edmonds et al. (2004a). The characteristic energy barrier of this diffusion process is estimated to be 1.4 eV. (Note that a factor of 2 was omitted in the original estimate of this energy by Edmonds et al. (2004a).)
Isolated MnI spectroscopy data are not available in (Ga,Mn)As, underlying the importance of theoretical work on the electric and magnetic nature of this impurity. Density functional calculations Ernst et al. (2005) suggest, e.g., that minority-spin MnI d states form a weakly dispersive band at ~ 0.5 eV below Fermi energy, a feature that is absent in the theoretical MnGa spectra. Ab initio total-energy calculations Máca and Mašek (2002); Mašek and Máca (2003) showed that Mn can occupy two metastable interstitial positions, both with a comparable energy, one surrounded by four Ga atoms (see Fig. 3) and the other surrounded by four As atoms. The two MnI states have similar local magnetic moments and electronegativity.
Calculations have confirmed that MnI acts as a double donor, as expected for a divalent metal atom occupying an interstitial position. Each interstitial Mn therefore compensates two substitutional Mn acceptors. It seems likely that because of the strong Coulombic attraction between positively charged MnI and negatively charged MnGa defects, mobile interstitials pair up with substitutional Mn during growth, as illustrated in Fig. 3 Blinowski and Kacman (2003). The total spin of a MnGa-MnI pair inferred from ab initio calculations is much smaller than the local spin S = 5∕2 of the isolated MnGa acceptor. This property, interpreted as a consequence of short-range antiferromagnetic interactions between two-local moment defects that have comparable local moments, has been confirmed experimentally Edmonds et al. (2005a). According to theory, the strength of this magnetic coupling contribution to the MnGa-MnI binding energy is 26 meV Mašek and Máca (2003).
Ab initio calculations of the valence-band spin splitting indicate that Jpd coupling constants of interstitial and substitutional Mn are comparable Mašek and Máca (2003). This would suggest a negligible net p-d coupling between the antiferromagnetically coupled MnGa-MnI pair and valence-band holes. We do note, however, that these LSDA calculations give Jpd ≈ 140 meV nm3, which is more than twice as large as the experimental value, and so this conclusion must be regarded somewhat cautiously. It is generally accepted that this discrepancy reflects the general tendency of the DFT LSDA and similar theories to systematically underestimate the splitting between occupied Mn d states in the valence-band continuum and empty Mn d states. Equation (2) illustrates how this deficiency of SDF band theories translates into an overestimated strength of the p-d exchange interaction. Apart from this quantitative inaccuracy, the relative strength of the p-d interaction of MnI compared to MnGa is still a somewhat controversial issue in the theoretical literature Blinowski and Kacman (2003); Mašek and Máca (2003), which has not yet been settled experimentally. This property and many others related to magnetism are sensitive to details of the SDF implementation to the way in which disorder is accounted for, and even to technical details associated with the way in which the Bloch-Schrödinger equation is solved numerically. For example, the positive charge of the MnGa-MnI (single-acceptor double-donor) pair, which will tend to reduce its exchange coupling with valence-band holes due to Coulomb repulsion, is not included in all approaches.
In addition to direct hole and local-moment compensation effects of MnI defects on ferromagnetism in (Ga,Mn)As, structural changes they induce in the crystal are indirectly related to important magnetic properties, particularly to the various magnetic and transport anisotropies. Ab initio theory predicts that the separation of the four nearest As neighbors surrounding the MnI in a relaxed lattice is increased by 1.5% compared to the clean GaAs lattice Mašek et al. (2003). Because of Coulomb repulsion between Ga cations and MnI defects, an even larger lattice expansion (~ 2.5%) is found for the MnI in the four Ga tetrahedral positions. When grown on a GaAs substrate, this effect of interstitial Mn leads to a lattice-matching compressive strain in the (Ga,Mn)As thin layers that induces a large uniaxial magnetic anisotropy, as discussed in detail in Section 5.3.
Low-temperature growth of GaAs is known to lead to the incorporation of high As antisite defect levels. This property is a combined consequence of the nonequilibrium growth conditions and As overpressure often used in the MBE process to assure the two-dimensional (2D) growth mode. These double-donor defects are likely to also be present the (Ga,Mn)As epilayers and may contribute to hole compensation.
Unlike MnI impurities, As antisites are stable up to ~450 ∘C Bliss et al. (1992). This is well above the temperature at which Mn precipitation starts to dominate the properties of (Ga,Mn)As and therefore As antisites cannot be removed from the epilayer by a postgrowth annealing treatment. Experimental studies suggest that the degradation of (Ga,Mn)As magnetic properties due to hole compensation by As antisites can be reduced by using As2 dimers instead of As4 tetramers and by maintaining a strictly stoichiometric growth mode Campion et al. (2003b).
The following elements of the qualitative picture of ferromagnetism in (Ga,Mn)As emerge from the experimental data and theoretical interpretations discussed in this section (see also Dietl (2002)). The low-energy degrees of freedom in (Ga,Mn)As materials are the orientations of Mn local moments and occupation numbers of acceptor levels near the top of the valence band. The number of local moments participating in the ordered state and the number of holes may differ from the number of MnGa impurities in the III-V host due to the presence of charge- and moment-compensating defects. Hybridization between Mn d orbitals and valence-band orbitals, mainly on neighboring As sites, leads to an antiferromagnetic interaction between the spins that they carry.
At low concentrations of substitutional Mn, the average distance between Mn impurities (or between holes bound to Mn ions) rc = (3∕4πNMn)1∕3 is much larger than the size of the bound hole characterized approximately by the impurity effective Bohr radius a* = εˉh∕m*e2. Here N Mn = 4x∕alc3 is the number of Mn impurities per unit volume, ε and alc are the semiconductor dielectric function and lattice constant, respectively, and m* is the effective mass near the top of the valence band. For this very dilute insulating limit, a theoretical concept was introduced in the late 1970s in which a ferromagnetic exchange interaction between Mn local moments is mediated by thermally activated band carriers Pashitskii and Ryabchenko (1979). Experimentally, ferromagnetism in (Ga,Mn)As is observed when Mn doping reaches approximately 1% Ohno (1999); Campion et al. (2003a); Potashnik et al. (2002) and the system is near the Mott insulator-to-metal transition, i.e., rc ≈ a* Marder (1999). At these larger Mn concentrations, the localization length of impurity-band states is extended to a degree that allows them to mediate ferromagnetic exchange interaction between Mn moments, even though the moments are dilute. Several approaches have been used to address ferromagnetism in DMSs near the metal-insulator transition (for a review see Dietl (2002); Timm (2003), including finite-size exact diagonalization studies of hole-hole and hole-impurity Coulomb interaction effects Timm et al. (2002); Yang and MacDonald (2003), and the picture of interacting bound magnetic polarons or holes hopping within the impurity band Inoue et al. (2000); Litvinov and Dugaev (2001); Durst et al. (2002); Chudnovskiy and Pfannkuche (2002); Kaminski and Das Sarma (2002); Berciu and Bhatt (2001); Bhatt et al. (2002); Alvarez et al. (2002). Because of the hopping nature of conduction and the mixed spd character of impurity-band states, the regime is sometimes regarded as an example of double-exchange ferromagnetism.
At even higher Mn concentrations, the impurity band gradually merges with the valence band Krstajić et al. (2004) and impurity states become delocalized. In these metallic (Ga,Mn)As ferromagnets, on which we focus in the following sections, the coupling between Mn local moments is mediated by the p-d kinetic-exchange mechanism Dietl et al. (1997); Matsukura et al. (1998); Jungwirth et al. (1999); Dietl et al. (2000); Jain et al. (2001). A qualitatively similar picture applies for (In,Mn)As and Mn-doped antimonides. In the metallic limit the influence of Coulomb and exchange disorder on perfect-crystal valence-band states can be treated perturbatively.
The crossover from impurity-band-mediated to Bloch valence-band-mediated interactions between Mn moments is a gradual one. In the middle of the crossover regime, it is not obvious which picture to use for a qualitative analysis, and quantitative calculations are not possible within either picture. Strongly localized impurity-band states away from Fermi energy may play a role in spectroscopic properties Okabayashi et al. (2001), even when they play a weaker role in magnetic and transport properties. The crossover is controlled not only by the Mn density but (because of the importance of Coulomb interaction screening) also by the carrier density. There is a stark distinction between the compensation dependence predicted by the impurity-band and Bloch valence-band pictures. When the impurity-band picture applies, ferromagnetism does not occur in the absence of compensation Kaminski and Das Sarma (2003); Das Sarma et al. (2003); Scarpulla et al. (2005) because the impurity band is filled. Given this, we can conclude from experiment that the impurity-band picture does not apply to optimally annealed (weakly compensated) samples which exhibit robust ferromagnetism.
The phenomenology of Mn-doped phosphide or nitride DMSs is more complex, with many aspects that probably cannot be captured by the Zener kinetic-exchange model Dietl et al. (2002); Krstajić et al. (2004). Experimentally, the nature of the Mn impurity is very sensitive to the presence of other impurities or defects in the lattice Korotkov et al. (2001); Graf et al. (2002, 2003a); Arkun et al. (2004); Edmonds et al. (2004c); Hwang et al. (2005). This substantially complicates the development of a consistent ferromagnetism picture in these materials. Larger p-d coupling in wide-gap DMSs (reported, e.g., in the photoemission experiment Hwang et al. (2005)), and stronger bonding of the hole to the Mn ion, might shift the metal-insulator transition to higher Mn densities. At typical dopings of several percent of Mn, the impurity band is still detached from the valence band Kronik et al. (2002), and ferromagnetic Mn-Mn coupling is mediated by holes hopping within the impurity band. Recent experiments indicate that this scenario may apply to (Ga,Mn)P with 6% Mn doping Scarpulla et al. (2005). LSDA calculations suggest Sanyal et al. (2003); Wierzbowska et al. (2004); Sandratskii et al. (2004) that p-d hybridization can be so strong that the admixture of Mn 3d spectral weight at the Fermi energy reaches a level at which the system effectively turns into a d-band metal. To illustrate this trend we show in Fig. 6 the LSDA and LDA+U calculations of the spin-split total density of states (DOS), and in Fig. 7 the results for the Mn d state projected DOS in (Ga,Mn)As and (Ga,Mn)N Sandratskii et al. (2004). Indeed, in the wider-gap (Ga,Mn)N the spectral weight of Mn d orbitals at the Fermi energy is large and is not suppressed even if strong on-site correlations are accounted for by introducing the phenomenological Hubbard parameter in the LDA+U method (see next section for details on combined Hubbard model and SDF techniques).
|
|
|
|
Another possible scenario for these more ionic III-P and III-N semiconductors, supported by EPR and optical absorption measurements and ab initio calculations Graf et al. (2002); Luo and Martin (2005); Kreissl et al. (1996); Schulthess et al. (2005), involves a transition of the substitutional Mn from a divalent (d5) impurity to a trivalent (d4) impurity. This strongly correlated d4 center, with four occupied d orbitals and a nondegenerate empty d level shifted deep into the host band gap, may form as a result of a spontaneous (Jahn-Teller) lowering of the cubic symmetry near the Mn site. If the energy difference between divalent and trivalent Mn impurity states is small, the DMS will have a mixed Mn valence which evokes the conventional double-exchange mechanism. Systems with dominant d4 character of Mn impurities, reminiscent of a charge-transfer insulator, will inevitably require additional charge co-doping to provide for ferromagnetic coupling between dilute Mn moments Schulthess et al. (2005).
Our focus is on the theory of (III,Mn)V ferromagnets and we therefore present in this section an overview of the different approaches that can be used to interpret the existing experimental literature and to predict the properties of materials that might be realized in the future. Since the electronic and magnetic properties of ferromagnetic semiconductors are extremely sensitive to defects that are difficult to control in real materials and may not be completely characterized, the ability to make reasonably reliable theoretical predictions that are informed by as many relevant considerations as possible can be valuable to discover useful new materials. For example, we would like to make confident predictions of the ferromagnetic transition temperature on a (III,Mn)V material as a function of the density of substitutional Mn, interstitial Mn, co-dopants, antisite defects, and any other defects whose importance might be appreciated in the future. This ability is developing, although there is no simple silver bullet that solves all difficulties for all host materials, and there may still be some considerations that are important for less studied host materials and are not yet part of the discussion. In this section we address in a general way the strengths and weaknesses of different theoretical approaches. The following sections of the review compare predictions made with different types of theoretical approaches with experimental data on a variety of important electronic and magnetic properties.
In SDF theory Hohenberg and Kohn (1964); Kohn and Sham (1965) many-body effects are buried in a complex exchange-correlation energy functional. Once an approximation is made for this functional, predictions for electronic and magnetic properties depend only on the particular arrangement of atomic nuclei under consideration. In principle nuclear positions can be relaxed to make sure that the spatial distribution of nuclei is metastable and therefore realizable. The exchange-correlation energy functional leads to a self-consistently determined spin-dependent exchange-correlation potential that appears in an effective independent-particle Hamiltonian. The main technical challenge in DFT applications is the development of numerically efficient methods that provide accurate solutions of single-body Schrödinger equations (see review articles Jones and Gunnarsson (1989); Sanvito et al. (2002)). DFT is established as a flexible and valuable tool for studying the microscopic origins of magnetism and for predicting electronic, magnetic, and ground-state structural properties in a wide variety of materials Jones and Gunnarsson (1989); Moruzzi and Marcus (1993). It has the advantage that it is a first-principles approach without any phenomenological parameters. DFT falls short of being a complete and general solution to the many-electron problem only because the exact form of the exchange-correlation energy functional is unknown. A simple and widely successful approximation is the LSDA von Barth and Hedin (1972).
The problem of solving LSDA equations with adequate accuracy remains a challenge even in perfectly ordered crystals. In DMSs the degrees of freedom that are important for ferromagnetism, the orientations of the Mn local moments, typically reside on approximately 1/40 of the atomic sites, which further complicates numerical implementation of the LSDA technique. Other length scales that are characteristic for the physics of interest in these materials, like the Fermi wavelengths of valence-band carriers, are also longer than the atomic length scale on which DFT interrogates matter. This property limits the number of independent magnetic degrees of freedom that can be included in a DFT simulation of DMS materials. The problem is exacerbated by the alloy disorder in (Ga,Mn)As. Even if all Mn atoms substitute for randomly chosen lattice sites, it is necessary to find a way to average over microrealizations of the alloy.
Disorder-averaging coherent-potential approximation (CPA) Soven (1967); Velický et al. (1968) and supercell approaches have been used successfully in combination with DFT calculations to address those physical parameters of (III,Mn)V DMSs that are derived from total-energy calculations, such as lattice constants, formation and binding energies of various defects, and type of magnetic order (see e.g. Park et al. (2000); van Schilfgaarde and Mryasov (2001); Sanvito et al. (2002); Máca and Mašek (2002); Erwin and Petukhov (2002); Sato et al. (2003); Edmonds et al. (2004a); Sandratskii et al. (2004); Wierzbowska et al. (2004); Mahadevan et al. (2004); Petit et al. (2006); Xu et al. (2005); Luo and Martin (2005)).
Supercell calculations have usually studied interactions between Mn moment orientations by comparing the energies of parallel-spin and opposite-spin orientation states in supercells that contain two Mn atoms. An effective spin Hamiltonian can be extracted from this approach if it is assumed that interactions are pairwise and of Heisenberg form. Even when these assumptions are valid, the interaction extracted from these calculations is the sum of interactions at a set of separations connected by the supercell lattice vector. If the Mn-Mn spin interaction has a range larger than a couple of lattice constants, this poses a problem for the supercell approach. Longer-range interactions can, however, be estimated using a spin-wave approach which allows spin-orientation variations that are incommensurate with the supercell. Effective interactions extracted in this way lead to a classical Heisenberg model from which the critical temperature can usually be calculated without substantial further approximation Sandratskii et al. (2004); Xu et al. (2005). The CPA approach can estimate the energy cost of flipping a single spin in the ferromagnetic ground state, which is proportional to the mean-field approximation for the critical temperature of the effective Heisenberg model Sandratskii et al. (2004); Sato et al. (2003), and in this sense is limited in its predictive powers when mean-field theory is not reliable. Alternatively, a more detailed picture of magnetic interactions is obtained by direct mapping of the CPA total energy to the Heisenberg Hamiltonian Kudrnovský et al. (2004); Liechtenstein et al. (1987); Bergqvist et al. (2004).
LSDA predictions for spectral properties, like the local DOS, are less reliable than predictions for total-energy-related properties. This is especially true for states above the Fermi energy, and is manifested by a notorious inaccuracy in predicting semiconductor band gaps. From a DFT point of view, this inconsistency arises from attempting to address the physics of quasiparticle excitations using ground-state DFT. In Mn-doped DMSs, the LSDA also fails to account for strong correlations that suppress fluctuations in the number of electrons in the d shell. One generally accepted consequence is that the energy splitting between the occupied and empty d states is underestimated in SDF theory, leading to an unrealistically large d-state local DOS near the top of the valence band and to an overestimate of the strength of the p-d exchange.
LDA+U Anisimov et al. (1991) and self-interaction-corrected (SIC) LSDA Perdew and Zunger (1981) schemes have been used to obtain more realistic energy spectra and help to establish theoretically microscopic origins of ferromagnetism in (III,Mn)V semiconductor alloys Park et al. (2000); Shick et al. (2004); Sandratskii et al. (2004); Petit et al. (2006); Filippetti et al. (2005); Wierzbowska et al. (2004); Schulthess et al. (2005). LDA+U schemes used in studies of (III,Mn)V DMSs combine SDF theory with the Hubbard description of strongly correlated localized orbitals. Additional parameters from the Hubbard model are added to the energy functional; they are obtained by fitting to experiment or, in principle, can be calculated self-consistently Anisimov et al. (1991). The SIC LSDA method is based on realizing that spurious self-interactions present in the SDF lead to unphysically large energy penalties for occupying localized states. Subtracting these interactions of a particle with itself from the density functional suppresses the tendency of the LSDA to delocalize strongly correlated atomic orbitals.
A practical approach that circumvents some of the complexities of this strongly correlated many-body problem is based on the Anderson many-body Hamiltonian theory Anderson (1961); Haldane and Anderson (1976); Fleurov and Kikoin (1976); Krstajić et al. (2004) and a tight-binding-approximation (TBA) band-structure theory Slater and Koster (1954); Harrison (1980). The TBA Hamiltonian includes the 8×8 sp3 term with second-neighbor-interaction integrals describing the host semiconductor Talwar and Ting (1982) and terms describing hybridization with nonmagnetic impurities and Mn. Effective single-particle TBA theory is obtained from the Anderson Hamiltonian by replacing the density operators in the Hubbard term in Eq. (1) with their mean values Mašek (1991). In the TBA model, local changes of the crystal potential at Mn and other impurity sites are represented by shifted atomic levels. The parameters chosen for the atomic-level shifts and hopping amplitudes between atoms can be inferred from experiment in a manner which corrects for some of the limitations with LSDA theory. The parametrization, summarized by Talwar and Ting (1982) and Mašek (1991), provides the correct band gap for the host crystal and appropriate exchange splitting of Mn d states. In the calculations, the hole density can be varied independently of Mn doping by adding nonmagnetic donors (e.g., Si or Se in GaAs) or acceptors (e.g. C or Be in GaAs).
Although the TBA model is a semiphenomenological theory, it shares with first-principles theories the advantage of treating disorder microscopically. A disadvantage of the tight-binding model approach, which is often combined with the CPA, is that it normally neglects Coulomb interaction effects which influence the charge and spin densities over several lattice constants surrounding Mn ion positions. Curie temperatures, magnetizations, the lifetimes of Bloch quasiparticle states, the effects of doping and disorder on the strength of p-d exchange coupling, and the effective Mn-Mn magnetic interaction are among the problems that have been analyzed using this tool Blinowski and Kacman (2003); Jungwirth et al. (2003a); Timm and MacDonald (2005); Jungwirth et al. (2005b,a); Sankowski and Kacman (2005); Vurgaftman and Meyer (2001); Tang and Flatté (2004).
The highest critical temperatures in (Ga,Mn)As DMSs are achieved in optimally annealed samples and at Mn doping levels above 1.5% for which band holes are itinerant, as evidenced by metallic conductivities Campion et al. (2003a). In this regime, semiphenomenological models that are built on crystal Bloch states rather than localized basis states for the band quasiparticles might be expected to provide more useful insights into magnetic and magnetotransport properties. A practical approach to this type of modeling starts from recognizing that the length scales associated with holes in DMS compounds are still long enough that a k ⋅ p, envelope function description of semiconductor valence bands is appropriate. Since for many properties it is necessary to incorporate spin-orbit coupling in a realistic way, six- or eight-band Kohn-Luttinger (KL) k ⋅ p Hamiltonians that include the spin-orbit split-off band are desirable Luttinger and Kohn (1955); Vurgaftman et al. (2001).
The kinetic-exchange effective Hamiltonian approach Zener (1951a); Bhattacharjee et al. (1983); Furdyna (1988); Dietl (1994) asserts the localized character of the five MnGa d orbitals, forming a moment S = 5∕2, and describes hole states in the valence band using the KL Hamiltonian and assuming the p-d exchange interaction between MnGa and hole spins. As discussed in Section 2.2.1, the exchange interaction follows from hybridization between Mn d orbitals and valence-band p orbitals. The approach implicitly assumes that a canonical transformation has been performed which eliminated the hybridization Schrieffer and Wolff (1966); Timm (2003). The k ⋅ p approximation applies when all relevant wave vectors are near the Brillouin-zone center and the model also assumes from the outset that states near the Fermi energy mainly have the character of the host semiconductor valence band, even in the neighborhood of a substitutional Mn. When these assumptions are valid it follows from symmetry considerations that the spin-dependent part of the effective coupling between Mn and band spins is an isotropic Heisenberg interaction characterized by a single parameter. If the KL Hamiltonian parameters are taken from the known values for the host III-V compound Vurgaftman et al. (2001), the strength of this exchange interaction Jpd can be extracted from one set of data, for example, from spectroscopic studies of isolated Mn acceptors as explained in Section 2.2.1, and used to predict all other properties Dietl et al. (1997); Matsukura et al. (1998); Jungwirth et al. (1999); Dietl et al. (2000); König et al. (2000). Since the value of Jpd can be obtained from experiments in a paramagnetic state the approach uses no free parameters to model ferromagnetism in these systems. In the absence of an external magnetic field the KL kinetic-exchange Hamiltonian has the general form
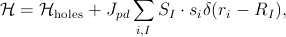 | (7) |
where ℋholes includes the k ⋅ p KL Hamiltonian and the interactions of holes with the random disorder potential and with other holes. The second term in Eq. (7) represents the p-d exchange interaction between local Mn spins SI and hole spins si.
The k ⋅ p approach has the advantage that it focuses on the magnetic degrees of freedom introduced by dilute moments, which can simplify analysis of the model’s properties. Disorder can be treated in the model by introducing Born-approximation lifetimes for Bloch states or by more sophisticated, exact-diagonalization or Monte Carlo methods Jungwirth et al. (2002a); König et al. (2003). This approach makes it possible to use standard electron-gas theory tools to account for hole-hole Coulomb interactions Jungwirth et al. (1999). The envelope function approximation is simply extended to model magnetic semiconductor heterostructures, like superlattices or quantum wells Lee et al. (2002); Kechrakos et al. (2005); Souma et al. (2005); Frustaglia et al. (2004); Brey and Guinea (2000); Lee et al. (2000). This strategy will fail, however, if the p-d exchange is too strong and the Mn acceptor level is correspondingly too spatially localized or too deep in the gap. For example, Mn-doped GaP and GaN compounds are likely less favorable for this approach than (III,Mn)As and (III,Mn)Sb compounds. Generally speaking, the advantages of a fully microscopic approach have increasing importance for more localized acceptors, and hence shorter-range Mn-Mn interactions, while the advantages of the k ⋅ p approach are more clear when acceptors are more shallow and Mn-Mn interactions have longer range.
There has also been theoretical work on (III,Mn)V DMS materials based on still simpler models in which holes are assumed to hop between Mn acceptor sites, where they interact with Mn moments via phenomenological exchange interactions Berciu and Bhatt (2001); Chudnovskiy and Pfannkuche (2002); Bhatt et al. (2002); Alvarez et al. (2002); Mayr et al. (2002); Fiete et al. (2003). Hamiltonians used in these studies have the form
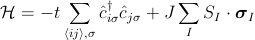 | (8) |
or something similar, where ĉiσ† creates a hole at site i with spin σ, the hole spin operator σI = ĉIα†σ αβĉIβ, and σαβ are the Pauli matrices. The models apply at least qualitatively in the low-Mn-density limit and are able to directly attack the complex and intriguing physics of these unusual insulating ferromagnets. Insulating ferromagnetism persists in this limit even when the carrier density is not strongly compensated Fiete et al. (2003). The dependence of ferromagnetism in this regime on the degree of compensation has not yet been systematically studied experimentally and seems certain to pose challenging theoretical questions. The models that have been used to study ferromagnetism in this regime can easily be adapted to include holes that are localized on ionized defects which may occur in addition to Mn acceptors.
Other related models assume that Mn acceptors are strongly compensated so that the density of localized holes is much smaller than the density of Mn ions, leading to a polaronic picture in which a single hole polarizes a cloud of Mn spins Kaminski and Das Sarma (2002); Durst et al. (2002). The free-parameter nature of these phenomenological models means that they have only qualitative predictive power. They are not appropriate for high-Tc (Ga,Mn)As materials which are heavily doped by weakly compensated Mn acceptors and are metallic. On the other hand, the impurity-band models may represent a useful approach to address experimental magnetic and transport properties of ferromagnetic (Ga,Mn)P where holes are more strongly localized Scarpulla et al. (2005); Kaminski and Das Sarma (2003); Das Sarma et al. (2003).
Experimental efforts to increase Mn doping in (Ga,Mn)As DMSs beyond the solubility limit of 0.1% have been assisted by modern ab initio theoretical studies of impurity formation energies and effects related to the growth kinetics Erwin and Petukhov (2002); Mašek et al. (2002); Mašek and Máca (2003); Mašek et al. (2004); Mahadevan and Zunger (2003); Edmonds et al. (2004a). Substitution of Ga by Mn is expected, based on these studies, to be enhanced when the Ga chemical potential is kept low relative to the Mn chemical potential, i.e., under Ga-poor, Mn-rich growth conditions Mahadevan and Zunger (2003). Calculations also suggest that one of the major drawbacks of bulk growth techniques is that they allow phase-separated precipitates, such as MnAs, to attain their most stable free-standing lattice geometry, leading to relatively low formation energies for these unwanted phases Mahadevan and Zunger (2003).
In thin-film epitaxy, competing phases are forced to adopt the crystal structure of the substrate, which can significantly increase their formation energies Mahadevan and Zunger (2003). Nonequilibrium LT MBE has been a particularly successful growth technique which allows a synthesis of single-phase (Ga,Mn)As DMSs with Mn concentrations up to ~ 10%. If the growth temperature is precisely controlled, a 2D growth mode of uniform DMSs can be maintained, and at the same time a large number of Mn atoms is incorporated in MnGa positions Foxon et al. (2004).
In (Ga,Mn)As DMSs a significant fraction of Mn atoms is also incorporated in interstitial positions Yu et al. (2002). Adsorption pathways that can funnel Mn to interstitial sites have been identified theoretically (see Fig. 8) using ab initio calculations of the potential-energy surface of Mn adsorbed on GaAs(001) Erwin and Petukhov (2002). First-principles calculations have also confirmed that interstitial MnI impurities are metastable in GaAs, showing that the three distinct positions they can occupy are two tetrahedral T (As4 or Ga4) positions surrounded by four near-neighbor As or Ga atoms, and one hexagonal position with three Ga and three As nearest neighbors. Among the three interstitial sites the hexagonal position is clearly less favorable, especially so in an overall p-type (Ga,Mn)As material Mašek and Máca (2003). The typical energy barrier for Mn diffusion between interstitial sites is approximately 1 eV Mašek and Máca (2003); Edmonds et al. (2004a). On the other hand, diffusion of Mn between Ga substitutional positions involves a kick-out mechanism of MnI + GaGa → MnGa + GaI for which the typical barrier is about 3 eV Erwin and Petukhov (2002). Interstitial MnI is therefore much more mobile than substitutional MnGa.
|
|
As mentioned in Section 2.3.1, MnI donors are likely to form near-neighbor pairs with MnGa acceptors in as-grown materials due to the strong Coulomb attraction. The net magnetic moment of such a pair is close to zero Blinowski and Kacman (2003); Mašek and Máca (2003); Edmonds et al. (2004a, 2005a). Although MnI can be removed by low-temperature annealing, the number of substitutional MnGa impurities will remain smaller than the total nominal Mn doping. The MnGa doping efficiency is therefore one of the key parameters that may limit the maximum Tc that can be achieved in (Ga,Mn)As epilayers, as we discuss in detail in Section 5.1. Ab initio calculations of the formation energies can be used to estimate the dependence of MnGa and MnI partial concentrations on total Mn doping in as-grown materials Mašek et al. (2004); Jungwirth et al. (2005b). Similarly, correlated doping effects can be studied for other defects that occur frequently in LT MBE (Ga,Mn)As materials, such as arsenic antisites AsGa Mašek et al. (2002).
Correlations between acceptors (MnGa) and donors (MnI or AsGa) in III-V semiconductors like GaAs are strong due to the nearly covalent nature of bonding in these crystals. The cohesion energy of covalent networks has a maximum if the Fermi energy EF lies within a band gap. Whenever EF is shifted to the valence band or conduction band the strength of bonds is reduced because of the occurrence of unfilled bonding states or occupied antibonding states, respectively.
In the case of weak doping, small changes in the impurity concentration can easily move EF across the band gap, with a negligible influence on the energy spectrum. The dependence of the formation energy, i.e., the energy cost for incorporating a particular impurity in a crystal, on the number of electrically active impurities can then be represented by the corresponding change in EF multiplied by the charge state of the impurity Mahadevan and Zunger (2003). In the case of strongly doped and mixed crystals, the redistribution of electronic states in the valence band due to impurities may play a more important role and should therefore be included in microscopic calculations.
In general, the formation energy as a function of impurity concentrations can be obtained from the composition-dependent cohesion energy Wcoh of the crystal. Assuming a sample consisting of N unit cells of the impure (mixed) crystal, the formation energy EA of an acceptor A replacing atom X is defined as the reaction energy of the substitution process,
sample + A -→ sample with one extra acceptor + X.
The corresponding reaction energy is
where Wtot(xA,xD) is the total energy of the doped crystal normalized to a unit cell, xA and xD are the acceptor and donor concentrations, and the last two terms represent the total energies of free-standing atoms X and A. With increasing size of the sample, N →∞, the first term in Eq. (9) approaches the derivative of Wtot(xA,xD) with respect to xA, and atomic energies can be absorbed using the relation between the total and cohesion energies. As a result, the cohesion energy represents a generating functional for the formation energies, i.e.,
 | (10) |
The formation energy of a donor D substituting for an atom Y has the same form with A ↔ D and X ↔ Y .
Having defined EA and ED, we note that in the low-concentration regime where they depend linearly on xA and xD,
 | (11) |
i.e., that the mutual influence of the two kinds of impurities is symmetric. K(xA,xD) in Eq. (11) plays the role of a correlation energy characterizing the co-doping process. For positive K(xA,xD), the formation energy of one impurity increases in the presence of the other. In this case the material tends to be either n type or p type rather than a compensated semiconductor. On the other hand, negative correlation energy indicates that the presence of impurities of one kind makes the incorporation of the other dopants easier. In this case compensation is favored.
Doping correlations over a wide and continuous range of impurity concentrations have been studied using the CPA, combined with either the parametrized TBA model or the ab initio linearized muffin-tin orbital (LMTO) DFT method Mašek et al. (2004); Jungwirth et al. (2005b). Results of these calculations are summarized in Figs. 9 and 10. The zero of energy is set to correspond to the formation energy of a reference Ga0.96Mn0.04As system with all Mn atoms occupying substitutional Ga positions. Four representative examples are considered here. SeAs and SiGa are typical single donors in GaAs that occupy the anion and cation sublattice, respectively. The As antisite defects AsGa and MnI interstitials are the most important native defects in (Ga,Mn)As, both acting as double donors. Figure 9 shows that the formation energy of MnGa decreases with increasing the number of donors. The curves are grouped into pairs according to the charge state of the donors, with only a minor influence of the particular chemical origin of the defect. The dependence is almost linear for low concentrations and the slope of the function is roughly proportional to the charge state of the donor. All this indicates that the variation of the formation energy of MnGa is mostly determined by the Fermi-level effect described above, and that the redistribution of the density of states induced by donor defects plays a minor role. Formation energies of the interstitial MnI in the tetrahedral T(As4) position are shown in Fig. 10. For the donor MnI impurity, the formation energy increases with the density of other donors. This means that the creation of MnI is efficiently inhibited in the presence of AsGa. Analogous results are obtained for AsGa antisite defects.
|
|
|
|
In Fig. 11 we show the change of formation energies of AsGa and MnI as a function of the number of MnGa. In both cases, the formation energy is a decreasing function of the density of MnGa. This self-compensation tendency is an important mechanism controlling the properties of as-grown (Ga,Mn)As mixed crystals. It explains the observed charge compensation in as-grown materials and is responsible to a large degree for the lattice expansion of highly Mn-doped (Ga,Mn)As DMSs, as we discuss in Section 4.2.
|
|
The formation energies can be used to theoretically estimate partial concentrations of substitutional MnGa, xs, and interstitial MnI, xi, in as-grown (Ga,Mn)As materials. An assumption is made in these calculations, whose validity is tested by a comparison with experimental data, that the probabilities of Mn atoms to occupy substitutional or interstitial positions are determined by the respective formation energies Es and Ei, even in the nonequilibrium LT-MBE-grown materials.
The balanced distribution of MnGa and MnI is reached when Mašek et al. (2002); Jungwirth et al. (2005b)
 | (12) |
as also expected from the growth point of view. Partial concentrations xs,i of Mn are obtained by solving Eq. (12) together with the condition 0 ≤ xs,i ≤ x, xs + xi = x. In Fig. 12 we show results of TBA CPA calculations Jungwirth et al. (2005b); for x > 1.5% xs ≈ 0.8x, and xi ≈ 0.2x. LMTO CPA theory calculations give very similar predictions Mašek et al. (2004).
Linear relations between xs, xi, and x reflect the fact that the difference of the formation energies of MnGa and MnI impurities (see inset of Fig. 12) can be, up to x = 10%, approximated by a linear function of xs and xi,
Equation (13) indicates that, for x < 1.5%, MnGa has a lower formation energy than MnI and Mn atoms tend to occupy substitutional positions. At and above x ≈ 1.5%, Δ(xs,xi) approaches zero and both MnGa and MnI are formed.The theoretical results are in very good agreement with experimental data, as shown in Fig. 12. The balance considerations, confirmed experimentally in samples with MnGa concentrations up to 6.8%, suggest that there is no fundamental physics barrier to increasing MnGa concentration up to 10% and beyond. Very precise control over the growth temperature and stoichiometry is, however, required for maintaining the 2D growth mode of the uniform (Ga,Mn)As materials at these high doping levels.
Finally, we note that during growth the formation energies control incorporation of Mn atoms, assuming that the total amount of Mn in the material is related to a sufficiently high chemical potential in the Mn source. The annealing processes, on the other hand, do not depend on the formation energies but rather on the energy barriers surrounding individual metastable positions of Mn in the lattice. The barriers are larger for MnGa Erwin and Petukhov (2002); Mašek and Máca (2003) so that postgrowth low-temperature annealing can be used to remove MnI without changing the number of MnGa significantly.
|
|
Changes in the lattice constant of (Ga,Mn)As DMSs, relative to the lattice constant of undoped GaAs, are too small to significantly suppress or enhance p-d kinetic exchange or other magnetic coupling mechanisms. Direct effects of doping-induced lattice distortion on the onset of ferromagnetism are therefore negligibly small. Nevertheless, variations in the lattice parameter provide a measure of impurity concentrations in the DMS material. The impurities do, of course, control ferromagnetism through their doping properties. Also, because thin-film (Ga,Mn)As epilayers are not relaxed, lattice-constant mismatch between the DMS layer and substrate induces strains that in many cases determine magnetocrystalline and magnetotransport anisotropies, as we discuss in detail in Sections 5.3.1 and 6.2. Theoretical calculations Mašek et al. (2003) of the dependence of the lattice constant on the density of the most common impurities in DMSs represent therefore another piece to the mosaic of our understanding of ferromagnetism in these complex systems.
Considering the values of the atomic radii of Mn (RMn = 1.17 Ĺ) and Ga (RGa = 1.25 Ĺ), the substitutional MnGa impurity may be expected to lead to only very small changes (reductions) in the lattice constant. This expectation is consistent with the calculated Zhao et al. (2002) lattice constant of a hypothetical zinc-blende MnAs crystal whose value is comparable to that of GaAs. On the other hand, As antisites produce an expansion of the GaAs lattice Liu et al. (1995); Staab et al. (2001) and a similar trend can be expected for interstitial Mn.
Modern density-functional techniques allow one to move beyond intuitive theoretical considerations and discuss the dependence of the lattice constant on impurity concentrations on a more quantitative level Mašek et al. (2003). The CPA is again a useful tool here for studying (Ga,Mn)As properties over a wide range of impurity concentrations. Some quantitative inaccuracies in theoretical results due to the limitations of the LMTO CPA approach (e.g., neglect of local lattice relaxations) have been corrected by using the full-potential linearized augmented-plane-wave supercell method Mašek and Máca (2005). Starting with an ideal (Ga,Mn)As mixed crystal with all Mn atoms occupying substitutional Ga positions, these calculations give the following Vegard’s law expression for the doping dependence of the lattice constant:
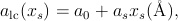 | (14) |
with the expansion coefficient as ranging from -0.05 to 0.02 depending on the method used in the calculation Mašek et al. (2003); Mašek and Máca (2005). As expected, a changes only weakly with the MnGa density xs.
A similar linear dependence is obtained for hypothetical crystals where AsGa (or MnI) is the only impurity present in the material, as shown in Fig. 13. According to the more reliable full-potential supercell calculations Mašek and Máca (2005), the composition-dependent lattice constant is found to obey
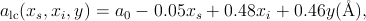 | (15) |
where xi and y are the densities of MnI and AsGa, respectively, and a0 is the lattice constant of pure GaAs.
|
|
Recently, several experimental works Potashnik et al. (2002); Kuryliszyn-Kudelska et al. (2004); Sadowski and Domagala (2004); Zhao et al. (2005) have studied the dependence of lattice constants in (Ga,Mn)As materials on disorder, based on a comparison between as-grown and annealed samples. Measurements confirmed that both AsGa and MnI defects lead to a significant expansion of the lattice. In samples grown under As-rich conditions, which are expected to inhibit formation of MnI impurities, annealing has virtually no effect on the measured lattice constant. This is consistent with the stability of AsGa defects up to temperatures that are far above the annealing temperatures. MnI impurities, on the other hand, can be efficiently removed by low-temperature annealing. Consistently, annealing leads to a significant reduction of the lattice constant in materials that contain a large number of these defects in the as-grown form, as shown in Fig. 14. On a quantitative level, experimental data suggest a stronger lattice expansion due to MnGa and a weaker expansion due to AsGa and MnI, compared to the theoretical predictions of Eq. (15). The quantitative disagreement can be attributed, in part, to the simplified description of the system within the theoretical model. Also, the presence of other lattice imperfections or inaccuracies in the determination of experimental doping values may have partly obscured the direct quantitative comparison between experiment and theory.
|
|
Curie temperatures in metallic (Ga,Mn)As have been studied theoretically starting from the k⋅p kinetic-exchange effective Hamiltonian Jungwirth et al. (1999); Dietl et al. (2000); Jungwirth et al. (2002b); Brey and Gómez-Santos (2003); Das Sarma et al. (2004); Jungwirth et al. (2005b) and from microscopic TBA or SDF band-structure calculations Sandratskii and Bruno (2002); Sato et al. (2003); Sandratskii et al. (2004); Hilbert and Nolting (2005); Jungwirth et al. (2003a); Timm and MacDonald (2005); Jungwirth et al. (2005b); Xu et al. (2005); Bouzerar et al. (2005a,b); Bergqvist et al. (2004, 2005). For a more detailed description of these theoretical approaches see Sections 3.1–3.3. The advantage of the k⋅p kinetic-exchange model is that it uses the experimental value for the p-d coupling constant Jpd, i.e., it correctly captures the strength of the magnetic interaction that has been established to play the key role in ferromagnetism in (Ga,Mn)As. The model also accounts for the strong spin-orbit interaction present in the host valence band, which splits the three p bands into a heavy-hole, light-hole, and split-off bands with different dispersions. The spin-orbit coupling was shown König et al. (2001a); Brey and Gómez-Santos (2003) to play an important role in suppressing magnetization fluctuation effects and therefore in stabilizing the ferromagnetic state up to high temperatures. On the other hand, describing the potentially complex behavior of MnGa in GaAs by a single parameter may oversimplify the problem. Calculations omit, for example, the suppression of Tc in low-hole-density (Ga,Mn)As materials due to the direct antiferromagnetic superexchange contribution to the coupling of near-neighbor Mn pairs. The whole model inevitably breaks down in DMS systems with holes strongly bound to Mn acceptors or with large charge fluctuations on MnGa d shells.
The advantage of microscopic approaches to Curie-temperature calculations is that they make no assumption about the character of MnGa impurities in GaAs and their magnetic coupling. They are therefore useful for studying material trends in Tc as a function of Mn doping or the density of other intentional or unintentional impurities and defects present in real systems. Because spin-orbit interactions add to the numerical complexity of calculations that are already challenging, they have normally been neglected in this approach. Another shortcoming, discussed already in Section 3.1, of LSDA approaches is an overestimated strength of the p-d exchange as compared to experiment. Within the mean-field approximation, which considers thermodynamics of an isolated Mn moment in an effective field and neglects correlated Mn-Mn fluctuations, microscopic calculations typically yield larger Tc’s than the effective Hamiltonian model, which uses the experimental value for Jpd. Stronger p-d exchange and the omission of spin-orbit coupling effects in the DFTs, however, also leads to a larger suppression of the Curie temperature due to fluctuation effects. (A closer agreement on the character of the Tc versus Mn-doping curves, calculated within the two formalisms, is obtained when the deficiencies of LSDA theories are partly eliminated by using, e.g., the LDA+U.) Despite the above weaknesses of semiphenomenological and microscopic calculations, a qualitatively consistent picture is clearly emerging from these complementary theoretical approaches that, as we discuss below, provides a useful framework for analyzing measured Tc’s.
Our review of theoretical Tc trends in (Ga,Mn)As starts with the results of the KL kinetic-exchange Hamiltonian and mean-field approximation to set up a scale of expected Curie temperatures. These estimates, which are not accurate in all regimes, are simplified by assuming a homogeneous distribution of MnGa ions and neglecting the role of other defects, apart from their potential contribution to hole or moment compensation Dietl et al. (2000, 1997); Jungwirth et al. (1999); König et al. (2003). For microscopic models this assumption is equivalent to the virtual-crystal approximation. Microscopic TBA calculations have shown very little effect of positional disorder on the strength of magnetic couplings in (Ga,Mn)As epilayers with metallic conductivities, partly justifying the virtual-crystal approach Jungwirth et al. (2003a). In addition, detailed theoretical studies confirm the absence of any significant magnetic frustration associated with the random positions of MnGa moments in the lattice in more metallic ferromagnetic semiconductors Timm and MacDonald (2005); Fiete et al. (2005). In the very dilute limit, however, Tc becomes sensitive to the distribution of Mn moments in the lattice Bergqvist et al. (2004).
In the mean-field approximation Jungwirth et al. (1999); Dietl et al. (2000), each local MnGa moment is described by a Hamiltonian SI ⋅ HMF where SI is the MnGa local spin operator, HMF = Jpd〈s〉, and 〈s〉 is the mean spin density of the valence-band holes (for the definition of the Jpd field, see Section 2.2.1). HMF is the effective field experienced by the local moments due to spin polarization of the band holes, analogous to the nuclear Knight shift. Similarly hMF = JpdNMn〈S〉 is the effective magnetic field experienced by the valence-band holes, which is proportional to the density and mean spin polarization of MnGa local moments. The dependence of 〈S〉 on temperature and field HMF is given König et al. (2003) by the Brillouin function Ashcroft and Mermin (1976)
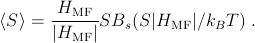 | (16) |
The Curie temperature is found by linearizing HMF and Bs around 〈S〉 = 0:
Here χf is the itinerant-hole spin susceptibility given by
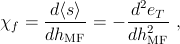 | (18) |
and eT is the total energy per volume of the holes. Equations (16) and (17) give
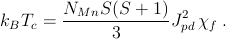 | (19) |
The qualitative implications of this Tc equation can be understood within a model itinerant-hole system with a single spin-split band and an effective mass m*. The kinetic energy contribution e k to the total energy of the band holes gives a susceptibility
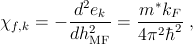 | (20) |
where kF is the Fermi wave vector. Within this approximation Tc is proportional to the MnGa local moment density, to the hole Fermi wave vector, i.e., to p1∕3 where p is the hole density, and to the hole effective mass m*.
A more quantitative prediction for the Curie temperature is obtained by evaluating the itinerant-hole susceptibility using a realistic band Hamiltonian,
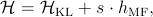 | (21) |
where ℋKL is the six-band KL Hamiltonian of the GaAs host band Vurgaftman et al. (2001) and s is the hole spin operator Dietl et al. (2000, 2001b); Abolfath et al. (2001a). The results, represented by the thick (black) line in Fig. 15, are consistent with the qualitative analysis based on the parabolic band model, i.e., Tc roughly follows the ~ xp1∕3 dependence. Based on these calculations, room-temperature ferromagnetism in (Ga,Mn)As is expected for 10% MnGa doping in weakly compensated samples Jungwirth et al. (2005b).
Hole-hole Coulomb interaction effects can be included in the lowest order of perturbation theory by adding the hole exchange contribution to the total energy Mahan (1981). The thin (red) line in Fig. 15 shows this Stoner Tc enhancement calculated numerically using the kinetic-exchange effective model with the six-band KL Hamiltonian. Tc stays roughly proportional to xp1∕3 even if hole-hole exchange interactions are included, and the enhancement of Tc due to interactions is of the order ~ 10–20% Jungwirth et al. (1999); Dietl et al. (2001b); Jungwirth et al. (2005b).
|
|
The mean-field effective Hamiltonian analysis above neglects discreteness in random MnGa positions in the lattice and magnetic coupling mechanisms additional to the kinetic-exchange contribution, particularly the near-neighbor superexchange. The former point can be expected to influence Tc at large hole densities, i.e., when the hole Fermi wavelength approaches interatomic distances. Of course, the entire phenomenological scheme fails on many fronts when the Fermi wavelength approaches atomic length scales since it is motivated by the assumption that all relevant length scales are long; the k⋅p band structure, the use of host material band parameters, and the neglect of momentum dependence in the Jpd parameter all become less reliable as the hole density increases to very large values. The approximations are apparently not fatal, however, even for x ~ 10% and any degree of compensation.
In the opposite limit of strongly compensated systems, where the overall magnitude of the hole-mediated exchange is weaker, antiferromagnetic superexchange can dominate the near-neighbor MnGa-MnGa coupling Kudrnovský et al. (2004), leading to a reduced Curie temperature Jungwirth et al. (2005b); Sandratskii et al. (2004). We emphasize that the k⋅p kinetic-exchange model cannot be applied consistently when nearest-neighbor interactions dominate, since it implicitly assumes that all length scales are longer than a lattice constant. We also note that net antiferromagnetic coupling of near-neighbor MnGa-MnGa pairs is expected only in systems with large charge compensations. In weakly compensated (Ga,Mn)As the ferromagnetic contribution takes over Kudrnovský et al. (2004); Mahadevan and Zunger (2004); Dietl et al. (2001b).
In addition to the above effects related to random Mn distribution, Mn positional disorder can directly modify p-d interactions when the coherence of Bloch states becomes significantly disturbed. Microscopic theories, such as the TBA and CPA Jungwirth et al. (2005b) or ab initio approaches based on either the CPA or supercell band structures Sandratskii et al. (2004); Sato et al. (2003), capture these effects on an equal footing and can be used to estimate trends in the mean-field Tc beyond the virtual-crystal approximation.
|
|
The mean-field CPA Curie temperatures are obtained by evaluating the energy cost of flipping one MnGa moment with all other moments held fixed in the ferromagnetic ground state. It can be evaluated for any given chemical composition Liechtenstein et al. (1987); Mašek (1991) and defines an effective exchange field Heff acting on the local moment. This energy change corresponds to HMF in the kinetic-exchange model used in the previous section, i.e.,
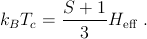 | (22) |
Results based on microscopic TBA band-structure calculations are shown in Fig. 16 as a function of hole density for several MnGa local-moment concentrations Jungwirth et al. (2005b). (The hole density is varied independently of MnGa doping in these calculations by adding nonmagnetic donors or acceptors.) Comparison with Fig. 15 identifies the main physical origins of the deviations from the Tc ~ xp1∕3 trend. Black dots in the left panel of Fig. 16 correspond to a relatively low local-MnGa-moment concentration (x = 2%) and hole densities ranging up to p = 4NMn, and show the expected suppression of Tc at large p. The effect of superexchange in the opposite limit is clearly seen when inspecting, e.g., the x = 10% data for p < 1 nm-3. The mean-field TBA CPA Curie temperature is largely suppressed here or even negative, meaning that the ferromagnetic state becomes unstable due to short-range antiferromagnetic coupling. Note that the neglect of Coulomb interactions in these TBA CPA calculations likely leads to an overestimated strength of the antiferromagnetic superexchange. The inhomogeneity of the carrier distribution in the disordered mixed crystal may also contribute to the steep decrease of Tc with increasing compensation seen in Fig. 16.
Although the Curie temperatures in the left panel of Fig. 16 appear to depart from the Tc ~ xp1∕3 dependence, the linearity with x is almost fully recovered when Tc is plotted as a function of the number of holes per MnGa local moment p∕NMn (see right panel of Fig. 16). Note that for compensations (1 - p∕NMn) reaching 100% this property of the superexchange coupling is reminiscent of the behavior of (II,Mn)VI diluted magnetic semiconductors Furdyna (1988) in which Mn acts as an isovalent magnetic impurity. The dependence on p in (Ga,Mn)As is expected to become very weak, however, when approaching the uncompensated state. Similarly, prospects for substantial increases in Tc by nonmagnetic acceptor co-doping of weakly compensated material appear to be quite limited.
In the left panel of Fig. 17 we show mean-field CPA Curie temperatures in uncompensated (p∕NMn = 1) (Ga,Mn)As DMSs as a function of Mn doping calculated using LDA and LDA+U ab initio methods. The LDA+U calculations, which give more realistic values of the p-d exchange coupling, confirm the linear dependence of Tc on x, showing no signs of saturation even at the largest doping x = 10% considered in these calculations.
|
|
The potential influence of correlated Mn-moment fluctuations (corrections
to mean-field theory) on ferromagnetic ordering in (Ga,Mn)As can be
recognized by considering, within a simple parabolic-band model, the RKKY
oscillation effect, which occurs as a consequence of the 2kF anomaly in the
wave-vector-dependent susceptibility of the hole system Dietl et al. (1997); Brey
and Gómez-Santos (2003). In this theory, which treats the hole system
perturbatively around the paramagnetic state, the sign of the hole-mediated
MnGa-MnGa coupling varies as cos(2kF d), where d is the distance between
MnGa moments, and its amplitude decays as d3. Estimating the average
MnGa-MnGa separation in a (Ga,Mn)As random alloy as 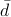 = 2(3∕4πNMn)1∕3 for
uncompensated (Ga,Mn)As systems and neglecting spin-orbit coupling
and band warping, cos(2kF
= 2(3∕4πNMn)1∕3 for
uncompensated (Ga,Mn)As systems and neglecting spin-orbit coupling
and band warping, cos(2kF 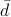 ) ≈-1, which means that the role of the
RKKY oscillations cannot be generally discarded. In realistic valence bands
oscillations are suppressed due to nonparabolic and anisotropic dispersions of
heavy- and light-hole bands and due to strong spin-orbit coupling Brey and
Gómez-Santos (2003); König et al. (2001a).
) ≈-1, which means that the role of the
RKKY oscillations cannot be generally discarded. In realistic valence bands
oscillations are suppressed due to nonparabolic and anisotropic dispersions of
heavy- and light-hole bands and due to strong spin-orbit coupling Brey and
Gómez-Santos (2003); König et al. (2001a).
More quantitatively, the range of reliability and corrections to the mean-field approximation in (Ga,Mn)As can be estimated by accounting for the suppression of the Curie temperature using the quantum theory of long-wavelength spin waves or using Monte Carlo simulations which treat Mn moments as classical variables. For weak p-d exchange coupling, SNMnJpd∕EF ≪ 1, where EF is the hole Fermi energy, the spin polarization of the hole system is small and the RKKY and spin-wave approximations treat collective Mn-moment fluctuations on a similar level. The advantage of spin-wave theory is that it can be used to explore the robustness of ferromagnetic states over a wider range of p-d couplings, including the more strongly exchange-coupled as-grown materials with large Mn density and large hole compensation (see Section 8.1 for a general discussion of magnetic interactions in the two coupling-strength limits).
Calculations in metallic systems have been performed starting from the k⋅p kinetic-exchange effective Hamiltonian Schliemann et al. (2001b); Brey and Gómez-Santos (2003); Jungwirth et al. (2005b) or from the SDF band-structure calculations Xu et al. (2005); Hilbert and Nolting (2005); Bouzerar et al. (2005a); Bergqvist et al. (2004). (Monte Carlo studies of Tc in the regime near the metal-insulator transition have been reported by Mayr et al. (2002).) Within a noninteracting spin-wave approximation, magnetization vanishes at the temperature where the number of excited spin waves equals the total spin of the ground state Jungwirth et al. (2002b, 2005b):
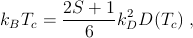 | (23) |
where kD = (6π2N Mn)1∕3 is the Debye cutoff and D(T) = D 0 〈S〉(T)∕S is proportional to the zero-temperature spin-wave stiffness parameter A (D0 = 2A∕SNMn) and the mean-field temperature-dependent average spin on Mn, 〈S〉(T) König et al. (2001a); Schliemann et al. (2001a). (For a detailed discussion of the micromagnetic parameter A, see Section 5.3).
Comparing the spin-stiffness results obtained using the k⋅p kinetic-exchange model with a simple parabolic band and with the more realistic spin-orbit-coupled KL Hamiltonian, the spin stiffness is observed to always be much larger in the KL model König et al. (2000, 2001a). For (Ga,Mn)As, the parabolic-band model underestimates D by a factor of ~10–30 for typical hole densities. This larger spin stiffness in spin-orbit-coupled valence bands is due to the heavy-hole–light-hole mixing. Crudely, the large-mass heavy-hole band dominates spin susceptibility and enables local (mean-field) magnetic order at high temperatures, while the dispersive light-hole band dominates spin stiffness and enables long-range magnetic order. The analysis highlights that the multiband character of the semiconductor valence band plays an important role in the ferromagnetism of (Ga,Mn)As.
Critical temperature estimates based on Eq. (23), the KL kinetic-exchange model, and including also the Stoner enhancement of Tc are summarized in Fig. 15 (blue symbols). These Tc estimates indicate that Tc will remain roughly proportional to x even at large dopings. The suppression of Tc due to spin waves increases with increasing hole density relative to the local moment concentration, resulting in saturation of the critical temperature with increasing p at about 50% compensation.
The suppression of Tc due to correlated Mn-moment fluctuations is also observed in LSDA calculations Xu et al. (2005); Hilbert and Nolting (2005); Bergqvist et al. (2004, 2005); Bouzerar et al. (2005a,b). The trend is illustrated in Fig. 18 where collective fluctuations are accounted for using spin-wave theory or the Monte Carlo approach Hilbert and Nolting (2005); Bergqvist et al. (2004); similar trends of suppressed mean-field Tc due to collective Mn-moment fluctuations have been predicted by spin-wave theory using a more elaborate, self-consistent random-phase approximation (RPA) technique on random lattice Bouzerar et al. (2005a). A larger suppression of the mean-field Tc seen in ab initio calculations, compared to KL kinetic-exchange model results, can be attributed partly to the simpler, threefold-degenerate LSDA valence-band structure in theories that neglect spin-orbit coupling. Also, the stronger p-d exchange in the LSDA theories may result in a weaker spin stiffness of the magnetic system, as holes are more strongly bound to Mn acceptors and the hole-mediated Mn-Mn coupling has a more short-range character. The enhancement of fluctuation effects in stronger p-d coupled systems is clearly seen in Fig. 18 when comparing LSDA results for narrower-gap (weaker p-d exchange) (Ga,Mn)As and wider-gap (stronger p-d exchange) (Ga,Mn)N.
|
|
Quantitative discrepancies between the KL kinetic-exchange model and LSDA results for the mean-field Tc and for the suppression of ferromagnetism due to collective Mn-moment fluctuations partly cancel out, leading to similar overall predictions for Curie temperatures in (Ga,Mn)As. Based on the Tc analysis alone it is therefore difficult to determine whether magnetic interactions have a short- or long-range character in (Ga,Mn)As DMSs.
Theoretically, the localization of the hole around the Mn impurity and the range of magnetic Mn-Mn interactions can be studied using microscopic TBA or ab initio calculations of the charge and moment distributions in the lattice or by mapping the total energy of the DMS crystal to the Heisenberg Hamiltonian van Schilfgaarde and Mryasov (2001); Sandratskii and Bruno (2002); Sato et al. (2003); Wierzbowska et al. (2004); Mahadevan and Zunger (2004); Kudrnovský et al. (2004); Hilbert and Nolting (2005); Schulthess et al. (2005); Timm and MacDonald (2005). Moving down the anion column in the periodic table from the nitride DMSs to antimonides, holes become more delocalized Mahadevan and Zunger (2004) and, consequently, Mn-Mn interactions are more long range in these microscopic calculations. In (Ga,Mn)As the LSDA theory predicts short-range magnetic coupling while the LDA+U or SIC-LSDA results suggest that holes which mediate the Mn-Mn exchange interaction are more delocalized van Schilfgaarde and Mryasov (2001); Wierzbowska et al. (2004); Schulthess et al. (2005).
Combined theoretical and experimental studies of remanent magnetization, micromagnetic parameters, and magnetotransport coefficients, discussed in Sections 5.2-7, indicate that in high-quality (Ga,Mn)As ferromagnets with metallic conductivities (conductivity increases with decreasing temperature) holes are sufficiently delocalized to make the kinetic-exchange model approach applicable. It is natural to expect that the free-carrier-mediated ferromagnetism picture will also apply in narrower-gap antimonide DMSs, such as (In,Mn)Sb, with even larger conductivities due to the smaller hole effective mass Wojtowicz et al. (2003). The smaller effective mass and larger unit-cell volume, as compared to arsenide DMSs, explain the smaller Curie temperatures in (III,Mn)Sb. This trend is illustrated in Table 1 by comparing the respective mean-field KL kinetic-exchange model Tc’s. In Mn-doped phosphides and nitrides the suppression of Tc due to effects beyond the mean-field virtual-crystal approximation, seen in LSDA calculations and related to the short-range nature of magnetic interactions, may prevail Scarpulla et al. (2005). We note also that LSDA Curie-temperature studies mentioned above do not capture the possible transition of the Mn impurity state in wide gap III-V semiconductors to the highly correlated trivalent (d4) center with four strongly localized d electrons and an empty d state deep in the gap, in which case the hole-mediated ferromagnetism picture implied by these calculations is not applicable Luo and Martin (2005); Kreissl et al. (1996); Schulthess et al. (2005).
|
|
Experimentally, Tc trends have been most extensively studied in (Ga,Mn)As Ohno (1998); Potashnik et al. (2002); Edmonds et al. (2002a); Yu et al. (2003); Chiba et al. (2003a); Ku et al. (2003); Stone et al. (2003); Jungwirth et al. (2005b). In Fig. 19 we show the temperature-dependent magnetization and inverse susceptibility of the current record Tc material Wang et al. (2005a). The Brillouin-function character of the magnetization curve confirms that the mean-field theory is appropriate in these high-quality DMS materials with metallic conductivities. The Curie temperatures for a series of as-grown and annealed (Ga,Mn)As samples with experimentally characterized charge and moment compensations are plotted in Fig. 20 Jungwirth et al. (2005b). The concentration of uncompensated Mn moments in the plot is xeff = xs - xi, where it is assumed that MnI donors present in the system are attracted to MnGa acceptors and that these pairs couples antiferromagnetically, as discussed in Sections 2.3.1 and 4.1. (The consistency of this assumption is confirmed by independent magnetization studies reviewed in Section 5.2.) The experimental Tc∕xeff plotted against p∕NMneff in Fig. 20, where N Mneff = 4x eff∕alc3, show a common Tc trend that is consistent with theoretical expectations Jungwirth et al. (2005b); Bouzerar et al. (2005a); Bergqvist et al. (2005). In particular, theory and experiment agree on the very weak dependence of Tc∕xeff on p∕NMneff for low compensation and the relatively rapid fall of Tc∕xeff with decreasing p∕NMneff for compensations of ~ 40% or larger. It should be noted that the maximum experimental xeff is only 4.6% in the as-grown sample and 6.8% after annealing for a total Mn concentration x = 9%, hence the modest Tc’s observed so far. Achieving Tc values close to room temperature in (Ga,Mn)As, which is expected to occur for xeff ≈ 10%, appears to be essentially a material growth issue, albeit a very challenging one Jungwirth et al. (2005b).
|
|
|
|
Only a few experimental studies of LT-MBE-grown (III,Mn)Sb DMSs have been reported to date Abe et al. (2000); Wojtowicz et al. (2003). The Curie temperatures measured in these materials are lower than the Tc’s in Mn-doped arsenides, consistent with kinetic-exchange model predictions in Table 1. The nature of ferromagnetism and therefore the interpretation of the experimental Curie temperatures observed in phosphide and nitride DMSs are not established yet, as already pointed out in Section 1.2.
In this section we focus on low-temperature ferromagnetic moments in (Ga,Mn)As DMSs with metallic conductivities. Early experimental studies, reporting large apparent magnetization deficits in (Ga,Mn)As Ohno and Matsukura (2001); Korzhavyi et al. (2002); Potashnik et al. (2002), motivated a theoretical search for possible intrinsic origins of frustrating magnetic interactions in this material. Using a wide spectrum of computational techniques, ranging from ab initio methods Korzhavyi et al. (2002); Mahadevan et al. (2004); Kudrnovský et al. (2004) and the microscopic TBA Timm and MacDonald (2005) to k⋅p kinetic-exchange models Schliemann and MacDonald (2002); Schliemann (2003); Brey and Gómez-Santos (2003); Zaránd and Jankó (2002); Fiete et al. (2005), theoretical studies have identified several mechanisms that can lead to noncollinear ground states. The observation that long-wavelength spin waves with negative energies frequently occur within the parabolic-band kinetic-exchange model illustrates that randomness in the distribution of Mn moments can result in an instability of the collinear ferromagnetic state Schliemann and MacDonald (2002). Frustration can be further enhanced when positional disorder is combined with anisotropies in Mn-Mn interactions. The pd character of electronic states forming the magnetic moment leads to magnetic interaction anisotropies with respect to the crystallographic orientation of the vector connecting two Mn moments Mahadevan et al. (2004); Kudrnovský et al. (2004); Timm and MacDonald (2005); Brey and Gómez-Santos (2003). When spin-orbit coupling is taken into account, magnetic interactions also become anisotropic with respect to the relative orientation of the Mn-Mn connecting vector and the magnetic moment Zaránd and Jankó (2002); Fiete et al. (2005); Schliemann (2003); Timm and MacDonald (2005).
Some degree of noncollinearity is inevitable as a combined consequence of positional disorder and spin-orbit coupling. Nevertheless, it was argued theoretically that a large suppression of ferromagnetic moment is not expected in metallic (Ga,Mn)As samples with Mn concentrations above ~ 1% Timm and MacDonald (2005). The minor role of noncollinearity is due largely to the long-range character of magnetic interactions, which tends to average out the frustrating effect of anisotropic coupling between randomly distributed Mn impurities Timm and MacDonald (2005); Zhou et al. (2004). Indeed, ab initio, microscopic TBA, and k⋅p kinetic-exchange model calculations of zero-temperature magnetic moments in (Ga,Mn)As ferromagnets which neglect effects that would lead to noncollinearity Dietl et al. (2001b); Wierzbowska et al. (2004); Schulthess et al. (2005); Jungwirth et al. (2005a) are consistent with experiments reported in a series of high-quality (Ga,Mn)As ferromagnets Edmonds et al. (2005a); Wang et al. (2005b); Jungwirth et al. (2005a). This rules out any marked intrinsic frustrations in the ground state of these DMSs. Substantial magnetization suppression seen in many early (Ga,Mn)As samples can be attributed primarily to the role played in those samples by interstitial Mn atoms and other unintentional defects.
We start the discussion by identifying the key physical considerations that influence the ground-state magnetization of (Ga,Mn)As ferromagnets by focusing on a single Mn(d5+hole) complex and approximating the total magnetization in the collinear state with a simple sum of individual (identical) Mn(d5+hole)-complex contributions. This crude model is used only to qualitatively clarify the connection between p-d hybridization and antiferromagnetic kinetic-exchange coupling, the sign of the hole contribution to total moment per Mn, and the expected mean-field contribution to magnetization per Mn from Mn local moments and from antiferromagnetically coupled holes. We also explain in this section that quantum fluctuations around the mean-field ground state are generically present because of the antiferromagnetic character of the p-d kinetic-exchange interaction.
Magnetization at T = 0 is defined thermodynamically by the dependence of the ground-state energy E on external magnetic field B:
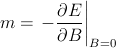 | (24) |
To avoid confusion that may result from using the hole picture to describe
magnetization of carriers in p-type (Ga,Mn)As materials, we recall first the
relationship between magnetizations evaluated using the physically direct electron
picture and magnetizations evaluated using the indirect but computationally more
convenient hole picture. In mean-field theory magnetization is related to the
change of single-particle energy with field, summed over all occupied orbitals.
Orbitals that decrease in energy with increasing field make a positive contribution
to the magnetization. For B ∥ + 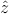 , the d-electron spins are aligned along
the (-z) direction (down spins) and the majority-spin-band electrons
have spin up due to antiferromagnetic p-d exchange coupling. Then, if
the majority band moves up in energy with B and the minority band
moves down, as illustrated in the left part of Fig. 21, the band kinetic
energy increases with B and, according to Eq. (24), the corresponding
contribution to the magnetization is negative. In the hole picture, we
obtain the same respective sense of the shifts of the majority-hole and
minority-hole bands, as illustrated in the right part of Fig. 21, and therefore the
correct sign of the magnetization (negative in our case). The cartoon
shows that in order to circumvent the potentially confusing notion of
the spin of a hole in magnetization calculations, it is safer to start from
the full Hamiltonian ℋ(B) in the physically direct picture of electron
states, where the sign of the coupling of the electron spin to the field and
the exchange energy are unambiguously defined. The electron picture →
hole picture transformation (ℋ(B) →-ℋ(B)) and the clearly defined
notion of majority and minority bands in either picture guarantees the sign
consistency of the calculated magnetization. Note that the language used here
neglects spin-orbit interactions, which lead to single-particle orbitals that do
not have definite spin character. Although spin-orbit interactions are
important they can be neglected in most qualitative considerations Jungwirth
et al. (2005a).
, the d-electron spins are aligned along
the (-z) direction (down spins) and the majority-spin-band electrons
have spin up due to antiferromagnetic p-d exchange coupling. Then, if
the majority band moves up in energy with B and the minority band
moves down, as illustrated in the left part of Fig. 21, the band kinetic
energy increases with B and, according to Eq. (24), the corresponding
contribution to the magnetization is negative. In the hole picture, we
obtain the same respective sense of the shifts of the majority-hole and
minority-hole bands, as illustrated in the right part of Fig. 21, and therefore the
correct sign of the magnetization (negative in our case). The cartoon
shows that in order to circumvent the potentially confusing notion of
the spin of a hole in magnetization calculations, it is safer to start from
the full Hamiltonian ℋ(B) in the physically direct picture of electron
states, where the sign of the coupling of the electron spin to the field and
the exchange energy are unambiguously defined. The electron picture →
hole picture transformation (ℋ(B) →-ℋ(B)) and the clearly defined
notion of majority and minority bands in either picture guarantees the sign
consistency of the calculated magnetization. Note that the language used here
neglects spin-orbit interactions, which lead to single-particle orbitals that do
not have definite spin character. Although spin-orbit interactions are
important they can be neglected in most qualitative considerations Jungwirth
et al. (2005a).
|
|
The electron-electron exchange energy has a negative sign and its magnitude increases monotonically when moving from the paramagnetic to the half-metallic (empty minority band) state. This together with Eq. (24) implies that the magnetization contribution from the electron-electron exchange energy has the same sign as the contribution from the kinetic energy. Using the same arguments as above we see that in the electron-electron exchange-energy case the sign of magnetization is also treated consistently by the electron picture → hole picture transformation.
The mean-field ground-state wave function of the Mn(d5+hole) complex is ∣Sz = -S〉∣jz = +j〉 and the magnetization per Mn is mMF = (gSS - gjj)μB, where S and j are local d-electron and hole moments and gS and gj are the respective Landé g factors. The five d electrons have zero total orbital angular momentum, i.e., gS = 2, and for the spin j = 1∕2 hole (gj = 2) we get mMF = 4μB. However, hole states near the valence-band edge have p character, so more realistically we should consider gjj = 4∕3 × 3∕2 = 2, which gives mMF = 3μB. We show below that this basic picture of a suppressed mMF due to holes applies also to highly-Mn-doped (Ga,Mn)As materials, although the magnitude of the mean-field hole contribution is weaker because of the occupation of both majority and minority hole bands and, partly, because of spin-orbit coupling effects.
The two-spin S and j model can also be used to demonstrate the presence of quantum fluctuations around the mean-field ground state, which is a consequence of the antiferromagnetic sign of the S ⋅ j coupling Jungwirth et al. (2005a). In the limit of B → 0 the two-spin Hamiltonian is given by
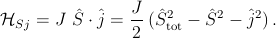 | (25) |
For antiferromagnetic coupling (J > 0), Stot = S -j, and the corresponding ground-state energy EAF = (∣J∣∕2)[(S - j)(S - j + 1) - S(S + 1) - j(j + 1)] = -∣J∣(Sj + j) is lower than the mean-field energy -∣J∣Sj. The mean-field ground state is not exact here and quantum fluctuation corrections to the magnetization will be nonzero in general. The difference between magnetizations of the exact and mean-field states is obtained from the corresponding expectation values of the Zeeman Hamiltonian gSμBBŜz + gjμBBĵz, and from Eq. (24) Jungwirth et al. (2005a):
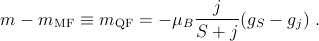 | (26) |
When j = 1∕2 and gS = gj = 2 the quantum fluctuation correction to the magnetization vanishes even though the mean-field ground state is not exact. The correction remains relatively weak also in the case of j = 3∕2 and gj = 4∕3, for which mQF = -0.25μB.
As in the Mn(d5+hole) complex, the magnetization of coupled-Mn-moment systems can be decomposed into mean-field contributions from Mn local moments and valence-band holes and a quantum fluctuation correction. At a mean-field level, the TBA description of (Ga,Mn)As mixed crystals is particularly useful for explaining the complementary role of local and itinerant moments in this p-type magnetic semiconductor and we therefore start by reviewing this approach Jungwirth et al. (2005a). In Fig. 22 the microscopic TBA CPA magnetic moments per Mn, mTBA, in (Ga,Mn)As ferromagnets are plotted as a function of p∕NMn. The value of mTBA is obtained here using the electron picture by integrating over occupied states up to the Fermi energy. Spin-orbit coupling is neglected in these TBA calculations and only the spin-polarization contribution to magnetization is considered in mTBA, which simplifies the qualitative discussion below.
A common way of microscopically separating contributions from local atomic and itinerant moments is by projecting occupied electron states onto Mn d and sp orbitals, respectively. In this decomposition, resulting local Mn moments are smaller than 5μB per Mn due to the admixture of d character in empty states near the valence-band edge. The effective kinetic-exchange model corresponds, however, to a different decomposition of contributions, in effect associating one spectral region with local Mn moments and a different spectral region with itinerant-hole moments. The kinetic-exchange model, in which local moments have S = 5∕2, is obtained from microscopic models, e.g. from the TBA and CPA, by expressing mTBA as the difference between a contribution mTBAint calculated by integrating over all electronic states up to midgap, i.e., including the entire valence band, and a contribution corresponding to the integral from the Fermi energy to midgap. As long as the valence-band–conduction-band gap is nonzero, the former contribution is independent of valence-band filling and equals the moment of an isolated Mn atom, 5μB. The latter term, plotted in the lower inset of Fig. 22, represents magnetization of itinerant holes.
|
|
The applicability of the kinetic-exchange model relies implicitly on the perturbative character of the microscopic p-d hybridization. The level of p-d hybridization over a typical doping range is illustrated in Fig. 23, which shows the orbital composition of mTBAint. The filled symbols are calculated including spectral weights from all spd orbitals while the half-open and open symbols are obtained after projecting onto d and sp orbitals, respectively. If there were no hybridization, mTBAint projected on d orbitals would equal the total mTBAint and the sp-orbital-projected m TBAint would vanish. In TBA CPA calculations, the d-orbital-projected mTBAint is reduced by only 10% as compared to the total mTBAint and therefore the p-d hybridization can be regarded as a weak perturbation. The nearly constant value of the d-orbital-projected mTBAint also suggests that the kinetic-exchange coupling parameter Jpd in the effective kinetic-exchange Hamiltonian is nearly independent of doping over the typical range of Mn and hole densities.
|
|
The decrease of mTBA in Fig. 22 with increasing p∕NMn clearly demonstrates the antiferromagnetic p-d exchange. The initial common slope for data corresponding to different Mn concentrations reflects the half-metallic nature of the hole system (only majority hole band occupied) when spin-orbit interactions are neglected. Here the hole contribution to magnetization per volume is proportional to p, i.e., magnetization per Mn is proportional to p∕NMn. The change in slope of mTBA at larger hole densities, which now becomes Mn-density dependent, reflects the population of the minority-spin hole band and therefore the additional dependence of hole magnetization on exchange splitting between majority- and minority-hole bands. Note that the maximum absolute value of the hole contribution to magnetization per hole (see upper inset of Fig. 22) observed in the half-metallic state is 1μB in these TBA calculations, which assume j = 1∕2 and gj = 2 holes.
Similar conclusions concerning the character of contributions to the magnetization of (Ga,Mn)As have been inferred from LDA+U and SIC LSDA supercell calculations Wierzbowska et al. (2004); Schulthess et al. (2005). (These microscopic calculations also neglect spin-orbit coupling.) The half-metallic LDA+U band structure in the case of zero charge compensation (p∕NMn = 1) results in a total magnetization per Mn of 4μB Wierzbowska et al. (2004), in agreement with the corresponding mTBA values. In SIC LSDA calculations Schulthess et al. (2005), the system is not completely half metallic and, consistently, the total moment per Mn is larger than 4μB. The LDA+U and SIC LSDA local moments on Mn are 4.7μB and 4.5μB, respectively, in good agreement again with the d-projected mTBAint values. In both ab initio calculations the oppositely aligned moment on the As sublattice extends over the entire supercell, confirming the delocalized character of holes and the antiferromagnetic sign of the p-d exchange.
The KL kinetic-exchange model calculations Dietl et al. (2001b); Jungwirth et al. (2005a) have been used to refine, quantitatively, predictions for the total magnetization based on the above microscopic theories. In particular, the number of minority holes at a given total hole density is underestimated in these TBA and ab initio approaches. This is caused in part by the quantitative value of the exchange spin splitting of the valence band which, e.g., in the TBA CPA calculations is a factor of 1.5–2 larger than the value inferred from experiment. Neglecting the spin-orbit interaction also results in three majority bands that are degenerate at the Γ point, instead of only two bands (heavy hole and light hole) in the more realistic spin-orbit-coupled band structure. (This deficiency is common to all calculations that neglect spin-orbit coupling.) In addition to having more states available in the majority band, which leads to underestimating the minority hole density, these microscopic calculations also omit the reduction of the mean spin density in the majority band caused by the spin-orbit coupling. The total magnetization values will be underestimated due to these effects. On the other hand, assuming only the spin contribution to the hole magnetization leads to an overestimated total magnetization, as already illustrated in Section 5.2.1.
In the kinetic-exchange effective model the T = 0 local-moment contribution to the magnetization per Mn is 5μB. As emphasized above, this is not in contradiction with the smaller d-electron contribution to the magnetic moment in microscopic calculations. The kinetic band energy contribution to the mean-field magnetization per Mn is obtained by numerically integrating over all occupied hole eigenstates of the Hamiltonian (21) and by finding the coefficient linear in B of this kinetic-energy contribution to the total energy Dietl et al. (2001b); Jungwirth et al. (2005a). Results of such calculations are summarized in Fig. 24, which shows the spin and orbital contributions to the magnetization of holes, and in Fig. 25, showing hole moment per Mn mMFkin for several local Mn-moment and hole densities. Note that the decoupling of the hole magnetization into spin and orbital terms is partly ambiguous in the spin-orbit-coupled valence bands and that only the total moment mMFkin has a clear physical meaning Dietl et al. (2001b); Jungwirth et al. (2005a). As expected holes give a negative contribution to magnetization, i.e., they suppress the total magnetic moment. The magnitude of the mean-field magnetization per hole ∣mMFkin∣N Mn∕p is smaller than 2μB obtained in Section 5.2.1 for the isolated spin-orbit-coupled hole bound to the Mn impurity. It is due to occupation of both majority and minority heavy- and light-hole bands at these typical (Ga,Mn)As hole densities (see inset of Fig. 25). Data shown in Fig. 24 and in the main panel of Fig. 25 indicate a ~(0.2–0.4)μB suppression of the mean-field moment per Mn due to the hole kinetic-energy contribution to magnetization.
|
|
|
|
The hole exchange energy contribution to the total mean-field magnetization was found to be negative and nearly independent of x and p in the typical doping range, and its magnitude is about a factor of 5 smaller than the magnitude of the term originating from the hole kinetic band energy Jungwirth et al. (2005a). Quantum fluctuation corrections lead to a 1% suppression of the mean-field moment per Mn Jungwirth et al. (2005a). (Details of these calculations, using the imaginary-time path-integral formulation of quantum many-body theory combined with the Holstein-Primakoff bosonic representation of the Mn local moments, can be found in König et al. (2001a) and Jungwirth et al. (2005a).) Combining all these considerations the T = 0 magnetization per Mn in the effective kinetic-exchange model has a positive mean-field contribution equal to 5μB from Mn local moments and a negative contribution from band holes and quantum fluctuations which suppress the moment per Mn by ~5–10 %.
The total magnetization per nominal Mn density and per effective density of uncompensated MnGa local moments has been measured by a superconducting quantum interference device (SQUID) in a series of as-grown and annealed (Ga,Mn)As samples Jungwirth et al. (2005a). The characterization of these materials has already been discussed in the previous section (see Fig. 20 and the related text). Within experimental uncertainty, the SQUID magnetization was found to be independent of the magnetization orientation, in agreement with theoretical expectations Jungwirth et al. (2005a). The moment decreases with increasing nominal Mn concentration, and increases on annealing Potashnik et al. (2002); Jungwirth et al. (2005a). This is consistent with the anticipated formation of interstitial Mn for doping above ~2% Jungwirth et al. (2005b), given the antiferromagnetic coupling between MnI and MnGa Blinowski and Kacman (2003); Edmonds et al. (2005a), and with breaking of this coupling by low-temperature annealing Yu et al. (2002); Edmonds et al. (2004a). In agreement with the above theoretical calculations, the total magnetization per effective density of uncompensated MnGa, mSQUIDeff, falls within the range (4–5)μB for all samples studied (See Fig. 26). Furthermore, although there is appreciable scatter, it can be seen that samples with lower hole densities tend to show higher mSQUIDeff, consistent with a negative contribution to magnetization from antiferromagnetically coupled band holes.
The local and d-state-projected contributions from Mn to the magnetic moment in (Ga,Mn)As have been probed experimentally by measuring the x-ray magnetic circular dichroism (XMCD) Edmonds et al. (2004b); Jungwirth et al. (2005a); Edmonds et al. (2005a). In agreement with the SQUID measurements and theoretical expectations, the XMCD data are independent, within experimental uncertainty, of the direction of magnetization Jungwirth et al. (2005a). The data are listed in Table 2 for two annealed samples with low and high Mn doping. In both cases, magnetic moments of around 4.5μB were obtained, showing a negligible dependence on the hole density. Similar results were found for samples with intermediate Mn doping Jungwirth et al. (2005a). Experimental XMCD results are in good agreement with corresponding TBA values indicated by half-open symbols in Fig. 23 and with LDA+U and SIC LSDA Mn local moments Wierzbowska et al. (2004); Schulthess et al. (2005). (Note that these microscopic calculations account only for the spin angular momentum contribution to the local Mn 3d moment since spin-orbit-coupling effects were neglected.)
|
|
|
A small set of parameters is often sufficient to phenomenologically describe the long-wavelength properties of ferromagnets. The description, which usually captures all properties that are relevant for applications of magnetic materials, starts from the micromagnetic energy functional e[n] of the spatially dependent magnetization orientation n = M∕M Aharoni (2001). The micromagnetic energy functional treats long-ranged magnetic dipole interactions explicitly and uses a gradient expansion for other terms in the energy. The magnitude M of the magnetization is one of the micromagnetic parameters characterizing the material. Zeroth-order terms in the energy functional are the magnetic anisotropy energy eani[n] and the Zeeman coupling to an external magnetic field if present, -μ0H ⋅ nM. The leading gradient term eex[n] referred to as the exchange energy in micromagnetic theory, represents the reduction in magnetic condensation energy when the magnetization orientation is not spatially constant. Micromagnetic parameters used to characterize the magnetic anisotropy energy depend on the symmetry of the system. For example, in a ferromagnet, which possesses uniaxial anisotropy with the easy axis aligned along the z direction, eani = Kunz2, where K u < 0 is the uniaxial anisotropy constant. As we explain below, the magnetic anisotropy of (Ga,Mn)As ferromagnets is a combination of the cubic term, the in-plane uniaxial anisotropy, and the uniaxial term induced by the growth-direction lattice-matching strain which often dominates in (Ga,Mn)As epilayers. Large anisotropies and relatively small magnetic moments of these dilute magnetic systems rank (Ga,Mn)As DMSs among hard ferromagnets (magnetic hardness parameter κ ~∣Ku∕μ0M2∣1∕2 > 1) with outstanding micromagnetic properties, including frequently observed single-domain-like characteristics of field-induced magnetization reversals Ohno (1998); Abolfath et al. (2001b); Dietl et al. (2001b); Potashnik et al. (2003); Wang et al. (2005d); Goennenwein et al. (2005).
Anisotropy of the exchange term in the micromagnetic functional is often neglected in which case it can be written as eex = A(∇n)2, where A is the spin-stiffness constant. The collective magnetization dynamics is described by the Landau-Lifshitz-Gilbert equation,
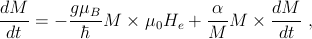 | (27) |
where μ0He = -∂e∕∂M and α is the Gilbert damping micromagnetic parameter. In this section we review KL kinetic-exchange model calculations for micromagnetic parameters of metallic (Ga,Mn)As ferromagnets Dietl et al. (2001b); Abolfath et al. (2001a); Dietl et al. (2001a); König et al. (2001a); Brey and Gómez-Santos (2003); Sinova et al. (2004b) and predictions based on the microscopic values of these parameters for anisotropy fields, the characteristic size of domains, and the critical current in current-induced magnetization switching Abolfath et al. (2001a); Dietl et al. (2001a); Sinova et al. (2004b).
Magnetocrystalline anisotropy, which is the dependence of the ferromagnet energy on the magnetization orientation with respect to the crystallographic axes, is a spin-orbit-coupling effect often associated with localized electrons in magnetic d or f shells. Local Mn moments in (Ga,Mn)As, however, are treated in the KL kinetic-exchange model as pure spins S = 5∕2 with angular momentum L = 0, and therefore do not contribute to anisotropy. The physical origin of the anisotropy energy in this model is spin-orbit coupling in the valence band Dietl (2001); Abolfath et al. (2001a). Even within the mean-field approximation to the KL kinetic-exchange model, magnetic anisotropy has a rich phenomenology which has explained a number of experimental observations in (III,Mn)V DMSs, including easy-axis reorientations as a function of hole density, temperature, or strains in the lattice Ohno et al. (1996a); Liu et al. (2003); Sawicki et al. (2004, 2005b); Masmanidis et al. (2005); Liu et al. (2004b).
The remarkable tunability of the magnetic properties of (Ga,Mn)As DMSs through lattice-matching strains is an important by-product of LT MBE growth of ferromagnetic films with lattices locked to those of their substrates in the plane perpendicular to the growth axis. X-ray-diffraction studies have established that the resulting strains are not relaxed by dislocations or other defects even for ~ 1-μm-thick epilayers Shen et al. (1999); Zhao et al. (2005). We mentioned in Section 4.2 that the lattice constant of relaxed (Ga,Mn)As is larger than the lattice constant of GaAs, especially if interstitial MnI or AsGa antisites are present in the DMS crystal. (Ga,Mn)As grown on a GaAs substrate is therefore under compressive strain. Tensile strained (Ga,Mn)As DMSs have been produced using (Ga,In)As substrates Ohno et al. (1996a); Shono et al. (2000); Liu et al. (2003).
Strain in the [001] growth direction breaks the cubic symmetry of (Ga,Mn)As resulting in a combined cubic and uniaxial anisotropy form of the energy functional,
Here Kc1 and Kc2 are the two lowest-order cubic anisotropy constants Dietl et al. (2001b); Abolfath et al. (2001a). Strain must be included in the k⋅p description in order to evaluate the uniaxial anisotropy constant Ku. For small strains this is done by expressing the positional vector r′ in the strained lattice in terms of r in the unstrained lattice as rα′ = r α + ∑ βeαβrβ, and expanding the KL Hamiltonian in lowest order of the strain constants eαβ Jones and March (1973); Chow and Koch (1999). In (Ga,Mn)As epilayers grown along the [001] direction, the strain constant exx = eyy can be tuned from approximately -1% to +1%. For larger strain values, the uniaxial term dominates the total anisotropy energy Dietl et al. (2001b); Abolfath et al. (2001a). In Fig. 27 we show mean-field KL kinetic-exchange model calculations of the uniaxial anisotropy field μ0Hu = ∣2Ku∕M∣ relative to the T = 0 magnetization M = gμBNMnS. μ0Hu corresponds to the minimum external magnetic field necessary to align the magnetization M along the hard axis. Figure (27) illustrates the dependence of the easy-axis orientation on the hole density and on the sign of exx. In particular, the easy axis is in plane for compressive strain (exx < 0) and out of plane for tensile strain (exx > 0), consistent with experiment Ohno et al. (1996a); Liu et al. (2003). The ability to manipulate the easy axis-orientation from in plane to out of plane has many implications for fundamental research on DMS materials and is very attractive also from the point of view of potential applications in magnetic recording technologies.|
|
(Ga,Mn)As epilayers have also a relatively strong in-plane uniaxial anisotropy component Liu et al. (2003); Sawicki et al. (2004, 2005b); Tang et al. (2003). The in-plane easy axis is consistently associated with particular crystallographic directions and can be rotated from the [110] direction to the [110] direction by low-temperature annealing. Although the origin of the in-plane uniaxial anisotropy has not been established, its dependence on hole concentration (varied by annealing) and temperature was modeled successfully within the KL kinetic-exchange model by assuming that it is associated with a small shear strain exy ≈ 0.05% Sawicki et al. (2005b).
Thermal and quantum magnetization fluctuation effects in metallic (Ga,Mn)As
DMSs have been described by Holstein-Primakoff boson representation of Mn
local spin operators. Assuming that fluctuations around the mean-field orientation
are small, the relationship between spin-raising and spin-lowering operators
and boson creation and annihilation operators is S+ = b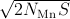 and
S- = b†
and
S- = b†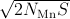 (Sx = (S+ + S-)∕2, S
y = (S+ -S-)∕2i) Auerbach (1994); König
et al. (2000, 2001a). After integrating out the itinerant-hole degrees of freedom
in the coherent-state path-integral formalism of the many-body problem, the
partition function
(Sx = (S+ + S-)∕2, S
y = (S+ -S-)∕2i) Auerbach (1994); König
et al. (2000, 2001a). After integrating out the itinerant-hole degrees of freedom
in the coherent-state path-integral formalism of the many-body problem, the
partition function
![∫
Z = 𝒟[ˉzz] exp(- Seff[zˉz])](review/auximages/review33x.png) | (29) |
depends only on the bosonic degrees of freedom (represented by the complex
numbers z and 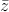 in the effective action Seff). The independent-spin-wave theory is
obtained by expanding Seff[
in the effective action Seff). The independent-spin-wave theory is
obtained by expanding Seff[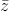 z] up to quadratic order in z and
z] up to quadratic order in z and 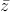 , i.e., spin
excitations are treated as noninteracting bosons. The spin-stiffness parameter A is
then calculated by fitting the microscopic spin-wave dispersion at long wavelength
by the form
, i.e., spin
excitations are treated as noninteracting bosons. The spin-stiffness parameter A is
then calculated by fitting the microscopic spin-wave dispersion at long wavelength
by the form
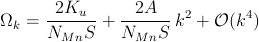 | (30) |
to match the conventions used for exchange and anisotropy constants in micromagnetic theory. Typical values of A in (Ga,Mn)As derived from the above many-body formalism and the KL kinetic-exchange description of hole bands are shown in Fig. 28. Values are consistent with the experimental spin-stiffness parameter in Ga0.949Mn0.051As measured by ferromagnetic resonance Goennenwein et al. (2003).
|
|
The damping of small-cone-angle magnetization precession in a ferromagnet is parametrized by the Gilbert coefficient. For small fluctuations of the Mn magnetization orientation in (Ga,Mn)As around the easy axis, Eq. (27) can be used to derive an expression for the linear response of a magnetic system to weak transverse fields in terms of the phenomenological constants of micromagnetic theory. For zero external static magnetic field and zero wave vector (uniform rotation), the corresponding inverse susceptibility reads
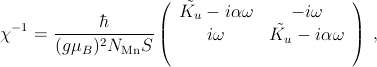 | (31) |
where 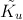 = Ku∕(ˉhNMnS) and ω is the frequency of the external rf field
perturbation.
= Ku∕(ˉhNMnS) and ω is the frequency of the external rf field
perturbation.
Microscopically, Gilbert damping in (Ga,Mn)As DMSs was attributed to the p-d exchange coupling between local Mn moments and itinerant holes Sinova et al. (2004b). The elementary process for this damping mechanism is one in which a local-moment magnon is annihilated by exchange interaction with a band hole that suffers a spin flip. This process cannot by itself change the total magnetic moment since the exchange Hamiltonian commutes with the total spin S + s. Net relaxation of the magnetization requires another independent process in which the itinerant-hole spin relaxes through spin-orbit interactions. A fully microscopic theory of the kinetic-exchange contribution to the Gilbert coefficient was derived by comparing Eq. (31) with microscopic linear response theory and by identifying the Gilbert coefficient with the dissipative part of the quantum-mechanical susceptibility Sinova et al. (2004b); Tserkovnyak et al. (2004),
![i
χRi,j(r,t∣r′,t′) = (gμB)2 -〈[Si(r,t),Sj(r ′,t′)]〉θ(t - t′).
ˉh](review/auximages/review40x.png) | (32) |
Here i = x,y and Si(r,t) = Mi(r,t)∕(gμB) are the Mn transverse spin-density operators. As in the microscopic theory of the spin stiffness, the correlation function (32) for the uniform (k = 0) precession mode was evaluated using the the long-wavelength noninteracting spin-wave form of the partition function (29) Sinova et al. (2004b). Gilbert coefficients in (Ga,Mn)As DMSs obtained within this formalism agree quantitatively with experimental values of α in homogeneous (annealed) systems measured from the width of the ferromagnetic resonance curves, as shown in Figs. 29 and 30.
|
|
|
|
Theoretical values of magnetic anisotropy and spin stiffness have been combined to estimate the typical domain size in tensile-strained (Ga,Mn)As epilayers with out-of-plane easy axis Dietl et al. (2001a). The calculated low-temperature width of a single-domain stripe of 1.1 μm compares favorably with the experimental value of 1.5 μm seen in the micro-Hall-probe experiments Shono et al. (2000). Near Tc the discrepancy between theoretical and experimental domain sizes becomes large, however, and has been attributed to critical fluctuation effects not included in the mean-field theory.
The calculated Gilbert damping coefficient and magnetic anisotropy constants were used to predict critical currents for spin-transfer magnetization switching Slonczewski (1996); Berger (1996) in (Ga,Mn)As-based tunneling structures Sinova et al. (2004b). Spin-polarized perpendicular-to-plane currents in magnetic multilayers with nonparallel spin configurations can transfer spin between magnetic layers and exert current-dependent torques Slonczewski (1996). The critical current for magnetization switching is obtained by adding the torque term to the Landau-Lifshitz-Gilbert equation (27) Slonczewski (1996); Sinova et al. (2004b). The critical currents ~ 105 A cm-2 obtained in these calculations and confirmed in experiment Chiba et al. (2004b) are two orders of magnitude smaller than those observed typically in metals. The small moment densities explain a large part of the orders of magnitude reduction in the critical current. This finding suggests that DMS materials have the potential to be particularly useful for exploiting the current-induced magnetization reversal effect in magnetic tunnel junctions.
Studies of the temperature-dependent resistivity, anisotropic magnetoresistance, and anomalous and ordinary Hall effects have been used to characterize DMS materials and to test different theoretical models describing these ferromagnets. In this section we review dc magnetotransport properties of (Ga,Mn)As focusing mainly on the metallic regime.
(Ga,Mn)As materials can exhibit insulating or metallic behavior depending on the doping and postgrowth-annealing procedures. (Strictly speaking, a material is defined as being metallic if its resistivity is finite in the limit T → 0, although for practical reasons this adjective is often used to describe a material whose resistivity decreases with increasing temperature over most or all of the range of temperatures studied in a particular series of experiments.) In optimally annealed samples with low density of unintentional defects, metallic behavior is observed for Mn doping larger than approximately 1.5% Campion et al. (2003a); Potashnik et al. (2002). In Section 2.4 we discussed this observation as a consequence of the Mott metal-insulator transition due to doping with substitutional MnGa acceptors. We also introduced in Sections 2.4 and 3.4 some of the theoretical work that has qualitatively addressed magnetic and transport properties of DMS systems near the metal-insulator transition. To our knowledge, a systematic experimental analysis has not yet been performed that would allow a reliable assessment of the theory predictions in this complex and intriguing regime. On the other hand, the dc transport in metallic (Ga,Mn)As DMSs has a rich phenomenology which has been explored in a number of experimental works and microscopic understanding of many of these effects is now well established.
LSDA CPA band-structure calculations combined with Kubo linear response theory were used to study correlations between the low-temperature conductivity and density of various defects in the lattice, the hole density, and Tc in metallic (Ga,Mn)As Turek et al. (2004). The theory tends to overestimate the conductivity in low-compensation materials but the overall range of values ~ 100–1000 Ω-1cm-1 for typical material parameters is consistent with measured data. As illustrated in Figs. 31 and 32, the theory models capture at a qualitative level the correlation between large conductivities and high Curie temperatures seen in experiment Campion et al. (2003a); Potashnik et al. (2002); Edmonds et al. (2002a). Comparable absolute values of the T = 0 conductance and similar trends in the dependence of the conductance on the density of impurities were obtained using the KL kinetic-exchange model and the semiclassical Boltzmann description of the dc transport Jungwirth et al. (2002a); López-Sancho and Brey (2003); Hwang and Das Sarma (2005). We note, however, that there are differences in the detailed microscopic mechanisms limiting the conductivity in the two theoretical approaches. Scattering in the ab initio theory is dominated by the p-d exchange potential on randomly distributed Mn atoms, and by local changes of the crystal potential on the impurity sites. Long-range Coulomb potentials produced by MnGa acceptors and other charged defects are omitted in the CPA approach.
|
|
|
|
In the kinetic-exchange effective Hamiltonian model elastic-scattering effects were included using the first-order Born approximation Jungwirth et al. (2002a). The corresponding transport-weighted scattering rate from the MnGa impurity has contributions from both the p-d exchange potential and the long-range Coulomb potential,
with scattering matrix elements Here εhost is the host semiconductor dielectric constant, ∣zi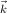 〉 is the
multicomponent eigenspinor of the KL Hamiltonian (21) and Ei,
〉 is the
multicomponent eigenspinor of the KL Hamiltonian (21) and Ei,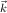 is the
corresponding eigenenergy, and the Thomas-Fermi screening wave vector
qTF =
is the
corresponding eigenenergy, and the Thomas-Fermi screening wave vector
qTF = 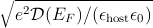 , where 𝒟(EF ) is the density of states at the Fermi
energy Jungwirth et al. (2002a). (Analogous expressions apply to scattering rates
due to other defects.)
, where 𝒟(EF ) is the density of states at the Fermi
energy Jungwirth et al. (2002a). (Analogous expressions apply to scattering rates
due to other defects.)
The relative strengths of scattering off the p-d exchange and Coulomb
potentials can be estimated by assuming a simple parabolic-band model
of the valence band characterized by the heavy-hole effective mass
m* = 0.5m
e. The p-d kinetic-exchange contribution in this approximation is
Γpd = NMnJpd2S2m*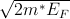 ∕(4πˉh4) and the scattering rate due to the screened
Coulomb potential ΓC is given by the standard Brooks-Herring formula
Brooks (1955). In (Ga,Mn)As with p = 0.4 nm-3 and x = 5%, these
estimates give ˉhΓpd ~ 20 meV and ˉhΓC ~ 150 meV. For lower compensation
(p ≈ 1 nm-3), the screening of the Coulomb potential is more efficient,
resulting in values of ΓC below 100 meV, but still several times larger
than Γpd. (Note that these elastic-scattering rates are smaller, although
by less than a factor of 10, than other characteristic energy scales such
as the Fermi energy and the spin-orbit-coupling strength in the GaAs
valence band which partly establishes the consistency of this theoretical
approach.)
∕(4πˉh4) and the scattering rate due to the screened
Coulomb potential ΓC is given by the standard Brooks-Herring formula
Brooks (1955). In (Ga,Mn)As with p = 0.4 nm-3 and x = 5%, these
estimates give ˉhΓpd ~ 20 meV and ˉhΓC ~ 150 meV. For lower compensation
(p ≈ 1 nm-3), the screening of the Coulomb potential is more efficient,
resulting in values of ΓC below 100 meV, but still several times larger
than Γpd. (Note that these elastic-scattering rates are smaller, although
by less than a factor of 10, than other characteristic energy scales such
as the Fermi energy and the spin-orbit-coupling strength in the GaAs
valence band which partly establishes the consistency of this theoretical
approach.)
The dominance of the Coulomb potential in Born approximation scattering rates for typical chemical compositions is confirmed by calculations based on the six-band KL Hamiltonian Jungwirth et al. (2002a). Good agreement between T = 0 conductivity values obtained using the ab initio and kinetic-exchange model theories should therefore be taken with caution as it may originate, to some extent, from the stronger local p-d exchange in the LSDA CPA theory, which partly compensates the neglect of long-range Coulomb potentials in this ab initio approach.
Boltzmann transport theory combined with the KL kinetic-exchange model of the (Ga,Mn)As band structure is a practical approach for studying magnetotransport effects that originate from the spin-orbit coupling. In Section 5.3 we reviewed the predictions of the model for the role of spin-orbit interaction in magnetic properties of (Ga,Mn)As. Here we focus on the anisotropic magnetoresistance (AMR) effect which is the transport analog of the magnetocrystalline anisotropy Wang et al. (2002); Baxter et al. (2002); Jungwirth et al. (2002a); Tang et al. (2003); Jungwirth et al. (2003b); Matsukura et al. (2004); Wang et al. (2005c); Goennenwein et al. (2005).
The AMR effect can be regarded as the first spintronic functionality implemented in microelectronic devices. AMR magnetic sensors replaced simple horseshoe magnets in hard-drive read heads in the early 1990s. With the introduction of giant-magnetoresistance-based devices in 1997, a new era was launched in the magnetic memory industry. In ferromagnetic metals, AMR has been known for well over a century. However, the role of the various mechanisms held responsible for the effect has not been fully clarified despite renewed interest motivated by practical applications Jaoul et al. (1977); Malozemoff (1985). The difficulty in metal ferromagnets partly stems from the relatively weak spin-orbit coupling compared to other relevant energy scales and the complex band structure. In (Ga,Mn)As ferromagnets with strongly spin-orbit-coupled holes occupying the top of the valence band, modeling of the AMR effect can be accomplished on a semiquantitative level without using free parameters, as we review below.
(Ga,Mn)As epilayers with broken cubic symmetry due to growth-direction lattice-matching strains are usually characterized by two AMR coefficients,
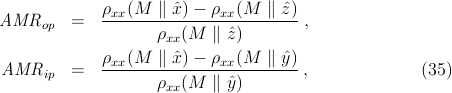
 . The three
different experimental configurations used to determine AMRop and AMRip are
illustrated in Fig. 33. The coefficient AMRip is given by combined effects of
spin-orbit coupling and current-induced broken symmetry between the two
in-plane cubic axes. The difference between AMRip and AMRop is a consequence
of the lowered symmetry in strained samples. Theoretical predictions for AMRip
and AMRop were compared with measurements in a series of (Ga,Mn)As epilayers
grown under compressive strain Jungwirth et al. (2003b). The calculated sign of
the AMR coefficients and the magnitude, which varies from ~ 1% in
highly-Mn-doped materials to ~ 10% in samples with low Mn concentration, are
consistent with experiment.
. The three
different experimental configurations used to determine AMRop and AMRip are
illustrated in Fig. 33. The coefficient AMRip is given by combined effects of
spin-orbit coupling and current-induced broken symmetry between the two
in-plane cubic axes. The difference between AMRip and AMRop is a consequence
of the lowered symmetry in strained samples. Theoretical predictions for AMRip
and AMRop were compared with measurements in a series of (Ga,Mn)As epilayers
grown under compressive strain Jungwirth et al. (2003b). The calculated sign of
the AMR coefficients and the magnitude, which varies from ~ 1% in
highly-Mn-doped materials to ~ 10% in samples with low Mn concentration, are
consistent with experiment. |
|
Reminiscent of the magnetocrystalline anisotropy behavior, the theory predicts
rotations as a function of the magnetization strain direction corresponding to the
high- (or low-) resistance state. Calculations illustrating this effect are
shown in Fig. 34 and the experimental demonstration in (Ga,Mn)As
epilayers with compressive and tensile strains is presented in Fig. 35.
In the top panel of Fig. 35, corresponding to (Ga,Mn)As material with
compressive strain, M ⊥ plane (M ∥ẑ) is the high-resistance configuration, the
intermediate-resistance state is realized for in-plane M ⊥ I (M ∥ŷ), and the
low-resistance state is measured when M ∥ I (M ∥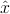 ). In the sample with
tensile strain, the in-plane M ⊥ I and M ⊥ plane curves switch places, as
seen in the bottom panel of Fig. 35. Consistent with these experimental
observations the theoretical AMRip and AMRop coefficients are negative and
∣AMRip∣ < ∣AMRop∣ for compressive strain and ∣AMRip∣ > ∣AMRop∣ for tensile
strain.
). In the sample with
tensile strain, the in-plane M ⊥ I and M ⊥ plane curves switch places, as
seen in the bottom panel of Fig. 35. Consistent with these experimental
observations the theoretical AMRip and AMRop coefficients are negative and
∣AMRip∣ < ∣AMRop∣ for compressive strain and ∣AMRip∣ > ∣AMRop∣ for tensile
strain.
|
|
|
|
The anomalous Hall effect (AHE) is another transport phenomenon originating from spin-orbit coupling which has been used to study and characterize ferromagnetic films for more than one hundred years Chien and Westgate (1980). The difficulties that have accompanied attempts at accurate microscopic description of the effect in metal ferromagnets are reminiscent of those in the AMR. The success of AHE modeling in (Ga,Mn)As materials Jungwirth et al. (2002c, 2003b); Edmonds et al. (2003); Dietl et al. (2003), reviewed in this section, has had implications also beyond the field of DMSs. It helped to motivate a reexamination of the AHE in transition metals and and in a series of more complex ferromagnetic compounds, which has led to a significant progress in resolving the microscopic mechanism responsible for the effect in these materials Yao et al. (2004); Fang et al. (2003); Lee et al. (2004); Dugaev et al. (2005); Kötzler and Gil (2005); Sinitsyn et al. (2005); Haldane (2004).
The Hall resistance Rxy ≡ ρxy∕d of a magnetic thin film of thickness d is empirically observed to contain two distinct contributions, Rxy = ROB + RAM Chien and Westgate (1980). The first contribution arises from the ordinary Hall effect (OHE) which is proportional to the applied magnetic field B, and the second term is the AHE which may remain finite at B = 0 and depends instead on the magnetization. RO and RA are the OHE and AHE coefficients, respectively. To put the AHE studies in DMSs in a broader perspective, the following discussion offers a brief excursion through the history of AHE theory and an overview of microscopic mechanisms discussed in this context in the literature (a more detailed survey is given by, e.g., Sinova et al. (2004a)).
The first detailed theoretical analysis of the AHE was given by Karplus and Luttinger Karplus and Luttinger (1954), where they considered the problem from a perturbative point of view (with respect to an applied electric field) and obtained a contribution to the anomalous Hall conductivity in systems with spin-orbit-coupled Bloch states given by
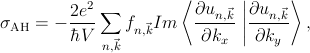 | (36) |
where fn,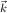 is the Fermi occupation number of the Bloch state ∣un,
is the Fermi occupation number of the Bloch state ∣un,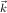 〉. This
contribution is purely a property of the perfect crystal and has become known in
recent years as the intrinsic AHE. It leads to an AHE coefficient RA proportional
to ρxx2 and therefore can dominate in metallic ferromagnets that have a relatively
large resistivity. The intrinsic AHE is related to Bloch-state Berry phases in
momentum space and depends nonperturbatively on the spin-orbit interaction
strength when degeneracies in momentum space are lifted by spin-orbit
coupling Sundaram and Niu (1999); Jungwirth et al. (2002c); Onoda and
Nagaosa (2002); Burkov and Balents (2003); Haldane (2004); Dugaev
et al. (2005). This point is particularly relevant for ferromagnetic semiconductors
because all carriers that contribute to transport are located near particular points
in the Brillouin zone, often high-symmetry points at which degeneracies
occur.
〉. This
contribution is purely a property of the perfect crystal and has become known in
recent years as the intrinsic AHE. It leads to an AHE coefficient RA proportional
to ρxx2 and therefore can dominate in metallic ferromagnets that have a relatively
large resistivity. The intrinsic AHE is related to Bloch-state Berry phases in
momentum space and depends nonperturbatively on the spin-orbit interaction
strength when degeneracies in momentum space are lifted by spin-orbit
coupling Sundaram and Niu (1999); Jungwirth et al. (2002c); Onoda and
Nagaosa (2002); Burkov and Balents (2003); Haldane (2004); Dugaev
et al. (2005). This point is particularly relevant for ferromagnetic semiconductors
because all carriers that contribute to transport are located near particular points
in the Brillouin zone, often high-symmetry points at which degeneracies
occur.
Shortly after the seminal work of Karplus and Luttinger, Smit proposed a different interpretation of the AHE based on a picture of asymmetric spin-dependent skew scattering off an impurity potential involving spin-orbit coupling Smit (1955); Nozieres and Lewiner (1973); Leroux-Hugon and Ghazali (1972). Analytically, the skew scattering appears in the second-order Born approximation applied to the collision term of the Boltzmann transport equation. This mechanism gives a contribution to RA ∝ ρxx, i.e., proportional to the density of scatterers, and dependent on the type and range of the impurity potential.
The AHE conductivity has a number of contributions in addition to the skew scattering and intrinsic contributions, which can originate from spin-orbit coupling in either the disorder scattering or the Bloch bands. Among these, side jump scattering has been identified as an important contribution Berger (1970). Side jumps due to spin-orbit coupling in Bloch bands appear as a ladder diagram vertex correction to the intrinsic anomalous Hall effect and their importance depends on the nature of that coupling Dugaev et al. (2005); Sinitsyn et al. (2005).
The ratio of intrinsic and skew-scattering contributions to the AHE conductivity can be approximated, assuming a single spin-orbit-coupled band and scattering off ionized impurities, by Leroux-Hugon and Ghazali (1972); Chazalviel (1975):
 | (37) |
where N∕p is the ratio of the density of ionized impurities and the carrier
density, rs is the average distance between carriers in units of the Bohr
radius, l is the mean free path, and c ~ 10, varying slightly with scattering
length. For the short-range scattering potential considered by Luttinger
Luttinger (1958) and Nozieres and Lewiner Nozieres and Lewiner (1973),
V (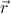 ) = V 0δ(
) = V 0δ(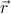 -
-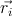 ):
):
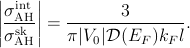 | (38) |
The estimate is a useful first guess at which mechanism dominates in different materials but one must keep in mind the simplicity of the models used to derive these expressions.
In (Ga,Mn)As, Eq. (37) gives a ratio of the intrinsic to skew-scattering contribution of the order of 50 and the intrinsic AHE is therefore likely to dominate Dietl et al. (2003). Consistently, the experimental RA in metallic (Ga,Mn)As DMSs is proportional to ρxx2 Edmonds et al. (2002b). Microscopic calculations of the intrinsic low-temperature AHE conductivity in (Ga,Mn)As were performed by taking into account the Berry-phase anomalous velocity term in the semiclassical Boltzmann equation leading to Eq. (36) Jungwirth et al. (2002c), and by applying the fully quantum-mechanical Kubo formalism Jungwirth et al. (2003b). In both approaches, the KL kinetic-exchange model was used to obtain the hole band structure.
In the Kubo formula, the dc Hall conductivity for noninteracting quasiparticles at zero external magnetic field is given by Onoda and Nagaosa (2002); Jungwirth et al. (2003b)
The real part of Eq. (39) in the limit of zero scattering rate (Γ → 0) can be written as Realizing that the momentum matrix elements 〈n′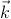 ∣
∣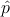 α∣n
α∣n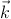 〉 = (m∕ˉh)〈n′
〉 = (m∕ˉh)〈n′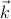 ∣∂ℋ(
∣∂ℋ(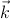 )∕∂α∣n
)∕∂α∣n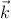 〉,
Eq. (40) can be shown to be equivalent to Eq. (36). The advantage of the Kubo
formalism is that it makes it possible to include finite lifetime broadening
of quasiparticles in the simulations. (See Section 6.2 for the discussion
of quasiparticle scattering rates in (Ga,Mn)As. Whether or not lifetime
broadening is included, the theoretical anomalous Hall conductivities are
of order 10 Ω-1 cm-1 for typical (Ga,Mn)As DMS parameters. On a
quantitative level, a nonzero Γ tends to enhance σAH at low Mn doping and
suppresses σAH at high Mn concentrations, where quasiparticle broadening due
to disorder becomes comparable to the strength of the kinetic-exchange
field.
〉,
Eq. (40) can be shown to be equivalent to Eq. (36). The advantage of the Kubo
formalism is that it makes it possible to include finite lifetime broadening
of quasiparticles in the simulations. (See Section 6.2 for the discussion
of quasiparticle scattering rates in (Ga,Mn)As. Whether or not lifetime
broadening is included, the theoretical anomalous Hall conductivities are
of order 10 Ω-1 cm-1 for typical (Ga,Mn)As DMS parameters. On a
quantitative level, a nonzero Γ tends to enhance σAH at low Mn doping and
suppresses σAH at high Mn concentrations, where quasiparticle broadening due
to disorder becomes comparable to the strength of the kinetic-exchange
field.
Systematic comparison between theoretical and experimental AHE data is shown in Fig. 36 Jungwirth et al. (2003b). Results are plotted versus nominal Mn concentration x while other parameters of the measured samples are listed in the legend. Experimental σAH values are indicated by filled squares and empty triangles correspond to theoretical data obtained for Γ = 0. Results shown in half-open triangles were obtained by solving the Kubo formula for σAH with nonzero Γ due to scattering off MnGa and As antisites, or MnGa and MnI impurities. Calculations explain much of the measured low-temperature AHE in metallic (Ga,Mn)As DMSs, especially so for the MnI compensation scenario. The largest quantitative discrepancy between theory and experiment is for the x = 8% material, which can be partly explained by a non-mean-field-like magnetic behavior of this specific, more disordered sample.
|
|
In DMSs the AHE has played a key role in establishing ferromagnetism and in providing evidence for hole-mediated coupling between Mn local moments Ohno et al. (1992); Ohno (1998). The dominance of the AHE in weak-field measurements (see Fig. 1) allows the Hall resistance to serve also as a convenient proxy for magnetization. On the other hand, the same property can obscure Hall measurements of the hole density. If magnetization is not fully saturated at low fields, for example, then ρAH = σAHρxx2 will increase with increasing external field B through the dependence of σAH on M(B), and hole densities derived from the slope of ρxy(B) will be too low. Accurate determination of hole densities in DMSs is essential, however, and the Hall effect is arguably the most common and accurate nondestructive tool for measuring the level of doping in semiconductors. Hall experiments performed in high magnetic fields to guarantee magnetization saturation seem a practical way for separating AHE contributions, especially in samples showing weak longitudinal magnetoresistance Ohno (1999); Edmonds et al. (2002b). Hole-density measurements performed using this technique assume that the Hall factor, rH = (ρxy(B) - ρAH)∕(B∕ep), with ρAH = ρxy(B = 0), is close to 1 despite the multiband spin-orbit-coupled nature of hole dispersion in (Ga,Mn)As ferromagnets. In the following paragraph we briefly review a theoretical analysis of this assumption Jungwirth et al. (2005b).
Microscopic calculations in nonmagnetic p-type GaAs with hole densities p ~ 1017–1020 cm-3 have shown that r H can vary between 0.87 and 1.75, depending on doping, scattering mechanisms, and the details of the model used for the GaAs valence band Kim and Majerfeld (1995). An estimate of the influence on rH from the spin splitting of the valence band and from the anomalous Hall term is based on the KL kinetic-exchange model description of the hole band structure. The Hall conductivity has been obtained by evaluating the Kubo formula at finite magnetic fields that includes both intraband and interband transitions. The approach captures the anomalous and ordinary Hall terms on equal footing Jungwirth et al. (2005a).
|
|
Many of the qualitative aspects of the numerical calculations, shown in Fig. 37, can be explained using a simple model of a conductor with two parabolic uncoupled bands. Note that the typical scattering rate in (Ga,Mn)As epilayers is ˉh∕τ ~ 100 meV and that the cyclotron energy at B = 5 T is ˉhω ~ 1 meV, i.e., the system is in the strong-scattering limit, ωτ ≪ 1. In this limit, the two-band model gives resistivities
where the indices 1 and 2 correspond to the first and second bands, respectively, the total density p = p1 + p2, and the zero-field conductivity σ0 = e2τp∕m*. Equation (41) suggests that in the strong-scattering limit the multiband nature of hole states in (Ga,Mn)As should not result in a strong longitudinal magnetoresistance. This observation is consistent with the measured weak dependence of ρxx on B for magnetic fields at which magnetization in the (Ga,Mn)As ferromagnet is saturated Edmonds et al. (2002b).The simple two-band model also suggests that the Hall factor rH is larger than 1 in multiband systems with different dispersions of individual bands. Indeed, for uncoupled valence bands, i.e., when accounting for intraband transitions only, the numerical Hall factors in the top panels of Fig. 37 are larger than 1 and independent of τ as also suggested by Eq. (41). The suppression of rH when spin-orbit coupling is turned on, shown in the same graphs, results partly from depopulation of the angular momentum j = 1∕2 split-off bands. In addition to this “two-band -model”-like effect, the inter-Landau-level matrix elements are reduced due to spin-orbit coupling since the spinor part of the eigenfunctions now varies with the Landau-level index. In ferromagnetic Ga1-xMnxAs bands are spin split and higher bands depopulated as x increases. In terms of rH, this effect competes with the increase of the inter-Landau-level matrix elements since spinors are now more closely aligned within a band due to the exchange field produced by polarized Mn moments. Increasing x can therefore lead to either an increase or a decrease in rH depending on other parameters, such as the hole density (compare top right panels of Fig. 37).
Interband transitions result in a more single-band-like character of the system, i.e., rH is reduced, and the slope of the ρxy(B) curve now depends more strongly on τ. Although the AHE and OHE contributions to ρxy cannot be simply decoupled, comparison of the numerical data in the four panels confirms the usual assumption that the AHE produces a field-independent offset proportional to magnetization and ρxx2. Comparison also suggests that after subtracting ρxy(B = 0), rH can be used to determine the hole density in (Ga,Mn)As with accuracy that is better than in nonmagnetic GaAs with comparable hole densities. For typical hole and Mn densities in experimental (Ga,Mn)As epilayers the error of the Hall measurement of p is estimated to be less than ±20% Jungwirth et al. (2005a).
Typical Fermi temperatures TF = EF ∕kB in ferromagnetic (Ga,Mn)As are much larger than the Curie temperature, relegating direct Fermi distribution effects of finite temperature to a minor role in transport. The carrier-mediated nature of ferromagnetism implies, however, strong indirect effects through the temperature dependence of the magnetization. A prime example is the AHE which from early studies of (III,Mn)V DMSs has served as a practical tool to accurately measure Curie temperatures Ohno et al. (1992). A rough estimate of Tc can also be inferred from the temperature-dependent longitudinal resistivity which exhibits a shoulder in more metallic (optimally annealed) samples and a peak in less metallic (as-grown) materials near the ferromagnetic transition Edmonds et al. (2002a); Potashnik et al. (2001); Van Esch et al. (1997); Matsukura et al. (1998); Hayashi et al. (1997). An example of this behavior is shown in Fig. 38 for a (Ga,Mn)As material with 8% nominal Mn doping Potashnik et al. (2001).
The shoulder in ρxx(T) has been qualitatively modeled using the mean-field, KL kinetic-exchange Hamiltonian given by Eq. (21). Solutions to the Boltzmann equation López-Sancho and Brey (2003); Hwang and Das Sarma (2005) are shown in Fig. 39. The temperature dependence of the longitudinal conductivity follows in this theory from variations in parameters derived from the spin-polarized hole band structure (e.g., Fermi wave vector) and from variations in screening of impurity Coulomb potentials.
|
|
The peak in resistance near Tc has been discussed in terms of scattering effects beyond the lowest-order Born approximation and by using a network resistor model Timm et al. (2005). It has also been suggested that this transport anomaly in more highly resistive DMSs is a consequence of the change in localization length caused by the ferromagnetic transition Zaránd et al. (2005).
|
|
Above the Curie temperature, measurements of ρxx have been used to estimate the value of Jpd. Assuming scattering off the p-d exchange potential at randomly distributed paramagnetic MnGa impurities and parabolic hole bands, the corresponding contribution to the resistivity is approximated by
![* 2 2
ρ = 2π2 kF-(m--)-JpdN [2χ (T,B) + χ (T,B)],
xx pe2 h3 Mn ⊥ ∥](review/auximages/review70x.png) | (42) |
where χ⊥ and χ∥ are the transverse and longitudinal magnetic susceptibilities Dietl (1994); Omiya et al. (2000); Matsukura et al. (2002). This theory overestimates critical scattering, particularly near the Curie temperature where the susceptibility diverges. Far from the transition on the paramagnetic side, however, fitting Eq. (42) to experimental magnetoresistance data gives an estimate of the Jpd Omiya et al. (2000) which is consistent with values inferred from spectroscopical measurements Okabayashi et al. (1998) (see Fig. 40).
|
|
Prospects for new technologies, based, for example, on materials in which the ferromagnetic transition can be controlled by light or on (III,Mn)V Faraday isolators monolithically integrated with existing semiconductor lasers, have motivated research in magneto-optical properties of DMSs Munekata et al. (1997); Koshihara et al. (1997); Sugano and Kojima (2000); Matsukura et al. (2002). Apart from these applied physics interests, ac probes have been used to study DMS materials with a wide range of experimental techniques. In Sections 2.2.1 and 5.2.2 we mentioned x-ray spectroscopies (core-level photoemission and XMCD) used to characterize Mn 3d states and detect the sign and magnitude of the p-d exchange coupling. Dispersions of hole bands in DMSs have been studied by angle-resolved photoemission with ultraviolet excitation Okabayashi et al. (2002, 2001); Asklund et al. (2002) and infrared-to-ultraviolet spectroscopic ellipsometry Burch et al. (2004). Raman scattering induced by excitations in the visible range was used as an alternative means of estimating hole densities Seong et al. (2002); Limmer et al. (2002); Sapega et al. (2001). Spectroscopic studies of isolated Mn(d5+hole) impurities in the infrared region provided key information on the valence of Mn in (Ga,Mn)As, as discussed in Section 2.2, and cyclotron resonance measurements were used to study highly-Mn-doped DMS materials in this frequency range Khodaparast et al. (2004); Sanders et al. (2003); Mitsumori et al. (2003). Microwave EPR and FMR experiments mentioned in Section 2.2 and 5.3 have been invaluable for understanding the nature of Mn in III-V hosts at low and high dopings and for characterizing magnetocrystalline anisotropies and magnetization dynamics in ferromagnetic materials. In this section we review some studies of the magneto-optical responses Ando et al. (1998); Kimel et al. (2005); Matsukura et al. (2002); Beschoten et al. (1999); Szczytko et al. (1999a); Hrabovsky et al. (2002); Lang et al. (2005), particularly magnetic circular dichroism (MCD), in the visible range and infrared absorption Singley et al. (2002, 2003); Hirakawa et al. (2002, 2001); Nagai et al. (2001); Szczytko et al. (1999a); Burch et al. (2005).
Optical absorption due to electron excitations across the band gap is a standard characterization technique in semiconductors. In (Ga,Mn)As, absorption occurs in the visible range and the position of its edge on the frequency axis depends on the circular polarization of incident light. Analysis of this magneto-optical effect provides information on the p-d exchange-induced band splitting and on doping in the DMS material Dietl (2002); Matsukura et al. (2002).
|
|
The schematic diagram in Fig. 41 shows that for a given sign of the exchange coupling the order of absorption edges corresponding to two circular photon polarizations can reverse in p-type materials, compared to systems with a completely filled valence band. Calculations for (Ga,Mn)As that include this Moss-Burnstein effect were carried out using the mean-field KL kinetic-exchange model Dietl et al. (2001b). The resulting absorptions α± of the σ± circularly polarized light, and MCD, defined as Sugano and Kojima (2000)
![α - - α+ Im[σxy(ω)]
M CD ≡ --+------= - -----------,
α + α Re[σxx(ω)]](review/auximages/review71x.png) | (43) |
are shown in Fig. 42. As suggested in the cartoon, the sign of the MCD signal in (Ga,Mn)As is opposite to the one obtained in bulk (II,Mn)VI DMSs where the sense of band splittings is the same as in (Ga,Mn)As but Mn substituting for the group-II element is an isovalent neutral impurity Dietl (1994). (The Moss-Burnstein sign change in MCD was also observed in co-doped p-type (II,Mn)VI quantum well Haury et al. (1997).)
|
|
Experimentally, the incorporation of several percent of Mn in GaAs enhances MCD, as shown in Fig. 43 Ando et al. (1998); Matsukura et al. (2002), and the sign of the signal near band-gap frequencies is consistent with the above theory which assumes antiferromagnetic p-d exchange coupling Ando et al. (1998); Beschoten et al. (1999); Szczytko et al. (1999a); Dietl et al. (2001b).
|
|
In (III,Mn)V DMSs, light absorption can occur at sub-band-gap frequencies due to excitations from the valence band to the Mn impurity band Hwang et al. (2002); Alvarez and Dagotto (2003); Craco et al. (2003) in more insulating materials and due to intra-valence-band excitations Sinova et al. (2002); Yang et al. (2003); Sinova et al. (2003) in more metallic systems, as illustrated schematically in Fig. 44. The infrared absorption associated with substitutional Mn impurities is spectrally resolved from higher-energy excitations to donor levels of the most common unintentional defects, such as MnI interstitials and AsGa antisites in (Ga,Mn)As, and therefore represents another valuable probe into intrinsic properties of these systems. Since infrared wavelengths are much larger than typical (submicron) DMS epilayer widths, the absorption is related to the real part of the conductivity by Sugano and Kojima (2000)
![Re[ σ(ω)]
α( ω) = 2--------- ,
Y + Y0](review/auximages/review72x.png) | (44) |
where Y and Y 0 are the admittances of the substrate and free space, respectively.
|
|
Model Hamiltonians (8) (see Section 3.4) combined with dynamical mean-field-theory or Monte Carlo simulations were used to study the role of the impurity band in infrared absorption Hwang et al. (2002); Alvarez and Dagotto (2003). In this theory, the impurity band forms when the strength of the model effective exchange interaction J is comparable to the width of the main band, characterized by the hopping parameter t. A non-Drude peak is observed in the frequency-dependent conductivity, associated with transitions from the main band to the impurity band. The behavior is illustrated in Fig. 45 together with the predicted temperature dependence of the absorption spectra obtained using the Monte Carlo technique. As discussed in Section 3.4, these model calculations are expected to apply to systems with strong p-d exchange coupling, like (Ga,Mn)P, and possibly also to (III,Mn)V DMSs, which are strongly compensated due to the presence of unintentional donor defects. (Impurity-band-mediated ferromagnetism does not occur in uncompensated samples.)
|
|
Theoretical infrared absorption spectra calculated using the k ⋅ p model for (Ga,Mn)As DMSs with delocalized holes in the semiconductor valence band, plotted in Fig. 46, show similar non-Drude characteristics with a peak near the excitation energy of 220 meV. The underlying physics is qualitatively different, however, as the peak in these KL kinetic-exchange model calculations originates from heavy-hole to light-hole intra-valence-band transitions Sinova et al. (2002). These results were obtained by evaluating the Kubo formula for ac conductivity assuming noninteracting holes and modeling disorder within the first-order Born approximation (see Eq. (33) in Section 6.1). In Fig. 47 we show theoretical predictions of exact-diagonalization studies based on the KL kinetic-exchange Hamiltonian but treating disorder effects exactly in a finite-size system. The results correct for the overestimated dc conductivity in the former model, which is a quantitative deficiency of the Born approximation as already mentioned in Section 6.1. At finite frequencies, the theoretical absorption in these metallic (Ga,Mn)As DMSs is almost insensitive to the way disorder is treated in the simulations, as seen from Figs. 46 and 47.
|
|
|
|
Experimental infrared absorption studies in ferromagnetic (Ga,Mn)As epilayers exhibit several common features summarized in Fig. 48 Singley et al. (2002, 2003); Hirakawa et al. (2002, 2001); Nagai et al. (2001); Szczytko et al. (1999a); Burch et al. (2005). Ferromagnetic materials (x = 5.2% curves in Fig. 48) show a non-Drude behavior in which the conductivity increases with increasing frequency in the interval between 0 and 220 meV, a broad absorption peak near 220–260 meV that becomes stronger as the sample is cooled, and a featureless absorption up to approximately 1 eV. As seen in Fig. 48, the peak is absent in the reference LT-MBE-grown GaAs sample confirming that the infrared absorption in ferromagnetic (Ga,Mn)As is related to changes induced by Mn impurities, in the band structure near the Fermi energy.
|
|
The presence of a finite-frequency peak in both impurity-band and KL kinetic-exchange models for the infrared conductivity leads to an ambiguity in the interpretation of existing data, which have for the most part been taken in as-grown, presumably heavily compensated material. The metallic behavior of the x = 5.2% material below Tc, seen in the lower panel of Fig. 48, favors the inter-valence-band absorption scenario. On the other hand, the large compensation likely present in as-grown low-Tc (Ga,Mn)As suggests that many holes may be strongly localized and that both absorption mechanisms may contribute to the measured absorption peak. Experiments in a series of samples interpolating between as-grown and optimally annealed limits, analogous to the resistance-monitored annealing studies Edmonds et al. (2002a, 2004a), should enable interpretation of infrared absorption spectra in (Ga,Mn)As DMSs. These studies will hint toward necessary refinements of the simplified theories used so far, e.g., inclusion of the energy dependence of Jpd and a more quantitative theory of the impurity-band model. The support for either scenario by these experiments has to be considered in conjunction with other available data in a self-consistent picture, e.g., in an impurity-band picture Tc is predicted to approach zero as the system reaches zero compensation, whereas the KL kinetic-exchange model has an opposite trend.
Systems with local moments coupled to itinerant electrons are common in condensed-matter physics and exhibit a wide variety of behaviors. Ferromagnets are far from the most common low-temperature states. For that reason it is useful to ask how (III,Mn)V materials, and (Ga,Mn)As with its robust ferromagnetic order in particular, fit in this larger context. This general qualitative analysis can help to identify some of the key factors that might limit the strength of ferromagnetic interactions in highly doped and strongly p-d-coupled DMS ferromagnets for which mean-field theory predicts the highest Curie temperatures.
An important class of materials that has been extensively studied is heavy fermions, in which f-electron local moments are exchange coupled to band electrons Stewart (1984). Kondo lattice models, which are believed to qualitatively describe heavy-fermion systems, assume that local moments exist at each lattice site. Models of DMS systems that make a virtual-crystal approximation (see Section 2.2.1and 5.1.1) place moments on all lattice sites and are therefore Kondo lattice models, often with specific details that attempt to capture some of the peculiarities of specific DMS materials. Theories of Kondo lattice model often start from a comparison of the RKKY (see Section 2.1) and Kondo temperature scales Doniach (1977); Degiorgi (1999); Tsunetsugu et al. (1997). The characteristic RKKY temperature refers to the strength of interactions between local moments mediated by a weakly disturbed carrier system and it is proportional to the mean-field Tc given by Eq. (19). The Kondo scale refers to the temperature below which strong correlations are established between an isolated local moment and the carrier system with which it interacts. Standard scale estimate formulas Doniach (1977) applied to the case of DMS ferromagnets imply that the Kondo scale is larger than the RKKY scale when the mean-field exchange coupling SNMnJpd is larger than the Fermi energy EF of the hole system, in other words, in the strong-coupling regime. The Kondo scale falls rapidly to small values at weaker coupling. (In heavy-fermion materials the Kondo temperature scale is larger than the RKKY temperature scale.)
|
|
Optimally annealed metallic (Ga,Mn)As materials are on the weak-coupling side of this boundary, but (Ga,Mn)N and possibly (Ga,Mn)P may be starting to reach toward the strong-coupling limit (if the simple S = 5∕2 local moment model still applies in these materials). As the strong-coupling limit is approached, quantum fluctuations (see discussion below Eq. (25)) will play a greater role, reducing the saturation moment per Mn and eventually driving down the ferromagnetic transition temperature. When the Kondo scale is much larger than the RKKY scale, the local moments are screened out by strongly correlated band electron spin fluctuations and effectively disappear before they have the opportunity to couple.
On the weak-coupling side, RKKY interactions in Kondo lattice models tend to lead to ferromagnetism only when the number of itinerant electrons per moment is small, i.e., only when at least the near-neighbor RKKY interaction is ferromagnetic Tsunetsugu et al. (1997). One of the surprising features of (Ga,Mn)As is the property that ferromagnetism still occurs when the number of itinerant electrons per moment is ~ 1. As mentioned in Section 5.1.2, this property follows from the specific multiband electronic structure and spin-orbit coupling at the top of the valence band. Nevertheless, frustrating antiferromagnetic RKKY interactions and exchange interactions that promote noncollinear magnetic states (see Section 5.2) will eventually become important for sufficiently large carrier densities. As this regime is approached from the ferromagnetic side, the transition temperature will be suppressed. These tendencies are summarized schematically in Fig. 49.
Similar considerations apply in assessing the robustness of ferromagnetism in the ordered state as characterized by the spin-stiffness micromagnetic parameter Schliemann et al. (2001a); König et al. (2001b, 2003). We used this approach in Section 5.1.1 when analyzing the limitations of the mean-field theory in (Ga,Mn)As. Starting from the ferromagnetic state, long-wavelength spin-orientation modulation will tend to lower the energy of some Mn-Mn interactions for sufficiently high carrier densities. The spin stiffness will weaken as the frustrated magnetism regime is approached, until finally the energy of ferromagnetic spin waves will become negative, signaling the instability of this state Schliemann and MacDonald (2002). Similarly, for sufficiently strong coupling, the band system will be fully (nearly when spin-orbit coupling is included) spin polarized and the cost of spin-orientation spatial variation will be borne mainly by the kinetic energy of the hole system and will no longer increase with exchange coupling. As shown schematically in the lower panel of Fig. 49, hole spins in this regime are locally antiferromagnetically locked to the fluctuating Mn moment orientations. For relatively small hole Fermi energies the kinetic-energy cost of these fluctuations is small, resulting in soft spin-wave excitations of the magnetic system König et al. (2001b). In this regime long-range ferromagnetic order disappears at temperatures smaller than the mean-field Tc, i.e., short-range order still exists above the Curie temperature.
The white bottom left area in the panels of Fig. 49 qualitatively depicts the parameter range in which the ferromagnetic RKKY mean-field state applies. Here Tc increases with the carrier density and local moment density, and (quadratically) with the strength of the p-d exchange coupling. For a fixed ratio of p∕NMn, increasing NMn corresponds to moving only slowly (as NMn1∕3) upward in the diagrams. This may explain why (Ga,Mn)As materials with larger Mn doping and with similar hole compensations as in ferromagnetic systems with low local-moment density do not show any marked weakening of the ferromagnetic state. With p∕NMn still fixed, attempts to increase Tc in (III,Mn)V DMSs by increasing the Jpd constant, in, e.g., ternary host alloys of Ga(As,P), might at some point reach the boundary of the soft spin-wave (Kondo screened) state. Similarly, the Kondo lattice model allows only a limited space for enhancing the robustness of the ferromagnetic state by tweaking the carrier and local-moment densities independently. In this case moving horizontally from the boundary of the frustrated RKKY (ferromagnetically unstable) state is accompanied by approaching vertically the soft spin-wave (Kondo screened) regime, and vice versa. Viewed from the opposite perspective, however, it is astonishing that a window in this parameter space has been found by the material research of (III,Mn)V compounds for robust DMS ferromagnets with Curie temperatures close to 200 K. The diagrams do not imply any general physical mechanism that limits Tc in these materials below room temperature.
Our remarks on the cartoons in Fig. 49 refer to the properties of Kondo lattice models that have been adjusted to reflect peculiarities of the zinc-blende semiconductor valence band. We have so far neglected the importance of disorder and Coulomb scattering in DMSs, and these can modify some parts of the simple qualitative picture depicted in Fig 49. This is particularly true in the very-low-density isolated Mn limit, i.e., the very strong exchange-coupling limit. Because of Coulomb attraction between valence-band holes and the charged Mn ion which carries the local moment, a total angular momentum F = 1 isolated bound state is created, as explained in Section 2.2.1, instead of the strongly correlated Kondo singlet. The importance of Coulomb interactions and disorder is lessened by screening and Pauli exclusion principle effects when both the Mn density and carrier density are high.
In this section we narrow down the discussion of magnetism in local-moment systems to semiconducting compounds, focusing on the phenomenology of ferromagnetic DMSs other than (III,Mn)V materials. Almost any semiconducting or insulating compound that contains elements with partially filled d or f shells (local moments) will order magnetically at a sufficiently low temperature. Semiconductors and insulators with high density of magnetic moments usually order antiferromagnetically, however, although ferromagnetism does occur in some cases. A famous example of a ferromagnetic system that can be regarded as a doped semiconductor is provided by the manganite family (e.g., La1-xSrxMnO3), whose ferromagnetism is favored by the double-exchange mechanism and occurs over a wide range of transition temperatures from below 100 to nearly 400 K. The onset of magnetic order in these systems is accompanied by a very large increase in conductivity. For a review, see, for example, Coey et al. (1999). Other well-known dense-moment (of order one moment per atom) ferromagnetic semiconductors with strong exchange interaction between itinerant and local spins include Eu and Cr chalcogenides Kasuya and Yanase (1968); Mauger and Godart (1986); Baltzer et al. (1966); van Stapele (1982), such as rock-salt EuO and spinel CdCr2Se4 with Curie temperatures 70 and 130 K, respectively.
DMS systems in which magnetic atoms are introduced as impurities have moments on only a small fraction of all atomic sites. The mechanisms that control magnetic order are therefore necessarily associated with the properties of these impurities. The coupling between moments will generally depend on locations of the dilute moments in the host lattice, on doping properties of the magnetic impurities, and on other dopants and defects present in the material. It seems plausible therefore that when DMS systems are ferromagnetic, their magnetic and magnetotransport properties will be more sensitive to material properties that can be engineered.
This review has concentrated on (Ga,Mn)As and related materials in which, as we have explained, substitutional Mn acts both as an acceptor and as a source of local moments. Ferromagnetism is carrier mediated and it has been demonstrated that it persists to surprisingly high temperatures. More may be achieved in the future by tweaking these materials. On the other hand, there is a vast array of alternate DMS materials that could be contemplated. Research to date has only scratched the surface of the volume of possibilities—we are truly still at the beginning of the road in studying diluted moment magnetism in semiconductors. Each system brings its new challenges. The interpretation of simple magnetic and transport characterization measurements is often not immediately obvious, in particular because of the possibility that the moments segregate into crystallites of one of a variety of available dense-moment minority phases which are often thermodynamically more stable. In addition, magnetic properties depend in general not only on the dilute moment density, which normally is well controlled and variable, but also on the partitioning of local moments among many available sites in the host crystal, which is not always known and is usually much harder to control. The search for promising DMS materials would be simplified if ab initio DFT methods had reliable predictive power. Unfortunately this luxury appears to be absent in many cases because of extreme sensitivity of magnetic properties to details of the electronic structure and because of strong-correlation effects that are often present in these systems. We mention briefly in the following some other classes of diluted magnetic semiconductors that have been studied.
The class of DMS ferromagnets that is closest to (III,Mn)V materials comprises the (II,Mn)VI compounds co-doped with group-V element acceptors. Examples include p-(Zn,Mn)Te:N Ferrand et al. (2001) and p-(Be,Mn)Te:N Hansen et al. (2001). These materials differ from (Ga,Mn)As mainly because the local moments and holes are provided by different types of impurities and can be controlled independently. Although the physics behind ferromagnetism seems to be very similar in the two classes of materials, the highest ferromagnetic transition temperatures that have been achieved are much smaller in the case of co-doped (II,Mn)VI materials, ~ 2 K rather than ~ 200 K. The difference is explained partly by difficulty in achieving the same extremely high hole doping (~ 1021 cm-3) in (II,Mn)VI materials that has been achieved in (Ga,Mn)As and partly by a favorable interplay between electrostatic and magnetic effects in (III,Mn)V materials. In (III,Mn)V materials, unlike (II,Mn)VI materials, the Mn moment is charged and attracts holes. The tendency of holes to have a higher density near Mn sites tends to increase the effective strength of the p-d exchange interaction. This effect is magnified when two Mn moments are on neighboring cation sites. In (Ga,Mn)As the interaction between Mn moments on neighboring cation positions is ferromagnetic, compared to the strongly antiferromagnetic interactions seen in (II,Mn)VI materials. (For a discussion of the interplay between electrostatic and magnetic interactions see Śliwa and Dietl (2005).) In p-doped (II,Mn)VI materials, competition between antiferromagnetic near-neighbor interactions and the longer-range carrier-mediated ferromagnetic interactions suppresses the magnetic ordering temperature. This competition apparently does not occur in (III,Mn)V ferromagnets with large hole densities.
(Zn,Mn)O is an interesting II-VI counterpart of the nitride III-V DMS Liu et al. (2005). With advances in oxide growth techniques, (Zn,Mn)O can be considered to be much like other (II,Mn)VI DMS materials and its investigation was originally motivated by theoretical work Dietl et al. (2000) that extrapolated from experience with (III,Mn)V DMS ferromagnets and predicted large Tc’s. Studies of this material have provided clear evidence of strong p-d exchange but so far have led to inconsistent conclusions about the occurrence of long-range magnetic order Sharma et al. (2003); Fukumura et al. (2005); Petit et al. (2006); Lawes et al. (2005).
Tetrahedral DMS materials doped with transition-metal atoms other than Mn have shown promising results. For instance, (Zn,Cr)Te is apparently homogeneous and has the required coupling between local moments and carriers Mac et al. (1996); Saito et al. (2003), and Curie temperatures as high as 300 K have been reported for this material. It may be, though, that the ferromagnetism is due to superexchange interactions rather than being carrier mediated since it occurs at very small ratios of the carrier density to the moment density Saito et al. (2002). Another interesting material with Cr moments is (Ga,Cr)N which exhibits ferromagnetism at ~ 900 K Liu et al. (2004a). The question still at issue in this material is the possible role of dense-moment precipitates.
Traditional groups of ferromagnetic DMSs also include (IV,Mn)VI solid solutions with the rock-salt structure Story et al. (1986, 1992); Eggenkamp et al. (1993). Although the band structures of IV-VI and III-V semiconductors are quite different, these DMS ferromagnets (e.g., (Pb,Sn,Mn)Te) appear to have a carrier-mediated mechanism quite similar to that of (Ga,Mn)As. Holes with densities up to 1021 cm-3 are supplied in these materials by cation vacancies, rather than by Mn substitution for divalent cations. The reported Curie temperatures in (Pb,Sn,Mn)Te are below 40 K Lazarczyk et al. (1997).
DMS ferromagnetism with Si or Ge as the host semiconductor is obviously attractive because of the greater compatibility of these materials with existing silicon-based technology. In Si, Mn impurities favor the interstitial position, which complicates the synthesis of a uniform DMS system. Mn in Ge, on the other hand, is a substitutional impurity and ferromagnetism has been reported in MBE-grown GexMn1-x thin-film DMSs Park et al. (2002); Li et al. (2005). Careful studies of GexMn1-x Li et al. (2005) have demonstrated that slow low-temperature growth is required to avoid the formation of thermodynamically stable dense-moment ferromagnetic precipitates; it is likely that the high-temperature ferromagnetism sometimes found in these materials is due to precipitates. The latest studies Li et al. (2005) appear to indicate that true long-range order in GexMn1-x emerges only at low temperatures ~ 12 K and that weak coupling between remote moments is mediated by holes which are tightly bound to Mn acceptors. Further work is necessary to determine whether this picture of magnetism, reminiscent of the polaronic physics discussed in the context of (Ga,Mn)P or low-carrier-density (III,Mn)V systems Scarpulla et al. (2005); Kaminski and Das Sarma (2003), applies to GexMn1-x DMSs.
The possible presence of dense-moment thermodynamically stable precipitates has also confused studies of oxide-semiconductor DMS systems. More consistent evidence of above-room-temperature ferromagnetism has been reported in Co-doped TiO2 although the origin of ferromagnetism in this material is still under debate (see, e.g., Matsumoto et al. (2001) and recent reviews Prellier et al. (2003); Fukumura et al. (2005)). Mn-doped indium tin oxide (ITO) is another promising candidate for a transparent ferromagnetic semiconductor which could be easily integrated into magneto-optical devices. Particularly encouraging is the observation of a large anomalous Hall effect showing that charge transport and magnetism are intimately connected in this oxide DMS Philip et al. (2004).
Other interesting related materials are the Mn-doped II-IV-V2 chalcopyrites surveyed theoretically in a first-principles calculation study by Erwin and Zutic (2004). Three of these compounds, CdGeP2, ZnGeP2, and ZnSnAs2, have shown ferromagnetism experimentally. The origin of this ferromagnetic behavior has not yet been explored extensively.
Finally we mention recent observations of ferromagnetic order up to ≈ 20 K in a layered semiconductor, Sb2Te3 doped with V or Cr Dyck et al. (2002, 2005). These highly anisotropic materials combine DMS behavior with strong thermoelectric effects. The character of the ferromagnetic coupling in these compounds is unclear at present.
This article is a review of theoretical progress that has been achieved in understanding ferromagnetism and related electronic properties in (III,Mn)V DMSs. The materials we have focused on have randomly located Mn(d5) local moments which interact via approximately isotropic exchange interactions with itinerant carriers in the semiconductor valence band. (Ga,Mn)As is the most thoroughly studied and best-understood system in this class. Some (III,Mn)V materials may exhibit fluctuations in the Mn valence between Mn(d5) and Mn(d4) configurations or have dominant Mn(d4) character, possibly (Ga,Mn)N, for example. Magnetic and other properties of materials in the latter class will differ qualitatively from those of (Ga,Mn)As and this review makes no attempt to discuss the theory that would describe them. When we refer to (III,Mn)V ferromagnetism below, it should be understood that any materials that prove to be in the latter class are excluded.
Interest in DMS ferromagnetism is motivated by the vision that it should be possible to engineer systems that combine many of the technologically useful features of ferromagnetic and semiconducting materials. This goal has been achieved to an impressive degree in (III,Mn)V DMSs, and further progress can be anticipated in the future. The goal of high-temperature semiconductor ferromagnetism flies in the face of fundamental physical limits, and the fact that so much progress has nevertheless been achieved is due to a serendipitous combination of attributes of (III,Mn)V materials. We have reserved the term “ferromagnetic semiconductor” for materials in which the coupling between local moments is mediated by carriers in the host semiconductor valence or conduction band. Then magnetic properties can be adjusted over a broad range simply by modifying the carrier system by doping, photodoping, gating, heterojunction band-structure engineering, or any technique that can be used to alter other semiconductor electronic properties. Most of these tuning knobs have already been established in (III,Mn)V ferromagnets.
Progress that has been made in achieving (Ga,Mn)As ferromagnetism and in understanding its phenomenology has a few lessons. The analysis of any DMS should start with understanding the properties of isolated defects associated with the magnetic element. In the case of (Ga,Mn)As materials the desirable magnetic defect is substitutional MnGa, because Mn then both introduces a local moment and acts as an acceptor. Holes doped in the system by MnGa impurities provide the glue that couples the moments together. Understanding the role of other defects that are present in real materials is also crucial. Substitutional MnI is particularly important in (Ga,Mn)As because it reduces the number of free moments and reduces the density of the hole gas that mediates ferromagnetism. Learning how to remove defects that are detrimental to strong magnetic order is key to creating useful materials. These two steps have been largely achieved in (Ga,Mn)As. There is every reason to believe that, if the same progress can be made in other DMS materials, some will be even more magnetically robust.
We have reviewed in this article a number of theoretical approaches that shed light on what controls key properties of ferromagnetic (III,Mn)V semiconductors. First-principles electronic structure calculations give a good overview of fundamental material trends across the series and explain many structural characteristics of these alloys. Semiphenomenological microscopic tight-binding models provide a convenient way to use experimental information to improve the quantitative accuracy of the description. Another phenomenological description that successfully models magnetic, magnetotransport, and magneto-optical properties is a single-parameter theory that adopts a k ⋅ p description for host semiconductor valence bands, and assumes that the exchange interaction between local moments and band electrons is short ranged and isotropic. The single exchange parameter that appears in this theory can be determined by fitting to known properties of an isolated Mn local moment, leading to parameter-free predictions for ferromagnetism. Qualitative models which focus on what kind of physics can occur generically for randomly located local moments that are exchange coupled to either localized or itinerant band electrons also provide useful insights for interpreting experiments.
The most important properties of (III,Mn)V materials are their Curie temperature and ferromagnetic moment, which reflect both the strength of the coupling between Mn local spins and its range. The highest ferromagnetic transition temperatures in (Ga,Mn)As epilayers have so far been achieved with substitutional MnGa fractions in the neighborhood of 5% by postgrowth annealing, which eliminates most interstitial Mn ions. Achieving Tc values close to room temperature in (Ga,Mn)As, which is expected to occur for 10% MnGa doping, appears to be essentially a material growth issue, albeit a very challenging one. In optimally annealed samples, experimental and theoretical considerations indicate that Mn-Mn exchange interactions are sufficiently long range to produce a magnetic state that is nearly collinear and insensitive to microrealization of the MnGa spatial distribution. Magnetization and Curie temperatures in these systems are well described by mean-field theory.
The magnetic and transport properties of high-quality (Ga,Mn)As materials are those of a low-moment-density, low-carrier-density metallic ferromagnet, with a few special twists. Because of the strong spin-orbit interactions in the valence band, metallic (Ga,Mn)As shows a large anomalous contribution to the Hall effect and the source of magnetic and transport anisotropies is more itinerant electrons, unlike the transition-metal case in which anisotropies originate primarily in d-electron spin-orbit interactions. The small moment densities lead to a large magnetic hardness, reflected in a single-domain-like behavior of many (Ga,Mn)As thin films. They also explain a large part of the orders of magnitude reduction in the current densities required for transport manipulation of the magnetic state through spin-momentum-transfer effects. The low-carrier density of the itinerant holes responsible for magnetic coupling means that they are concentrated around a particular portion of the Brillouin zone in the valence band which has a large oscillator strength for optical transitions to the conduction band. This property opens up opportunities for optical manipulation of the magnetic state that do not exist in transition-metal ferromagnets and have not yet been fully explored. The research reviewed here that is aimed at an understanding of the optical properties of (Ga,Mn)As ferromagnets is still incomplete, particularly for ideal annealed materials, and will be important in setting the groundwork for the exploration of new effects.
These conclusions do not necessarily apply to all (III,Mn)V ferromagnets. For example, material trends suggest that wider-band-gap hosts would have stronger exchange scattering that would lower the conductivity, shorten the range of Mn-Mn exchange interactions, and increase the importance of quantum fluctuations in Mn and band-hole spin orientations. This could eventually lead to Curie temperatures significantly below the mean-field estimates. In the opposite limit, when the exchange interaction is weak enough to be treated perturbatively, sign variations in the RKKY Mn-Mn interaction are expected to lead to frustration and weaken ferromagnetism at large carrier densities. One of the important miracles of (Ga,Mn)As ferromagnetism is that this effect is much weaker than would naively be expected because of the complex valence-band structure. In (Ga,Mn)As, incipient frustration that limits magnetic stiffness may be responsible for the weak dependence of the ferromagnetic transition temperature on carrier density. This property of (Ga,Mn)As suggests that little progress on the Tc front is likely to be gained by nonmagnetic acceptor co-doping.
Disorder is an inevitable part of the physics of all DMS ferromagnets because of the random substitution of elements possessing moments for host semiconductor elements. Even in metallic, ideal annealed samples that have only substitutional MnGa impurities, randomness in the Mn microstructure leads to both Coulomb and spin-dependent exchange potential scattering. For (Ga,Mn)As, Coulomb scattering dominates over exchange potential scattering, limiting the conductivity to ~ 100–1000 Ω-1cm-1. Frustration and disorder are certainly very important near the onset of ferromagnetism at low Mn density, where the network of exchange interactions that lead to long-range order is still tenuous. Studies of well-characterized materials with low Mn fraction near the metal-insulator transition are now possible because of progress in understanding the role of defects and are likely to exhibit complex interplay between the disorder and the Coulomb and exchange interactions.
We thank all colleagues who have given us the permission to show their results in this review. Among the many stimulating discussions we would like to especially acknowledge our interactions with experimentalists at the University of Nottingham. Work on the article was supported by by the Grant Agency of the Czech Republic through Grant No. 202/05/0575, by the Academy of Sciences of the Czech Republic through Institutional Support No. AV0Z10100521, by the Ministry of Education of the Czech Republic Center for Fundamental Research LC510, by the U.K. EPSRC through No. Grant GR/S81407/01, by the Welch Foundation, by the U.S. Department of Energy under Grant No. DE-FG03-02ER45958, and by the U.S. Office of Naval Research under Grant No. ONR-N000140610122.
Abe, E., F. Matsukura, H. Yasuda, Y. Ohno, and H. Ohno, 2000, Physica E 7, 981.
Abolfath, M., T. Jungwirth, J. Brum, and A. H. MacDonald, 2001a, Phys. Rev. B 63, 054418.
Abolfath, M., T. Jungwirth, and A. H. MacDonald, 2001b, Physica E 10, 161.
Akai, H., 1998, Phys. Rev. Lett. 81, 3002.
Almeleh, N., and B. Goldstein, 1962, Phys. Rev. 128, 1568.
Alvarez, G., and E. Dagotto, 2003, Phys. Rev. B 68, 045202.
Alvarez, G., M. Mayr, and E. Dagotto, 2002, Phys. Rev. Lett. 89, 277202.
Anderson, P. W., 1950, Phys. Rev. 79, 350.
Anderson, P. W., 1961, Phys. Rev. 124, 41.
Ando, K., T. Hayashi, M. Tanaka, and A. Twardowski, 1998, J. Appl. Phys. 83, 6548.
Anisimov, V. I., J. Zaanen, and O. K. Andersen, 1991, Phys. Rev. B 44, 943.
Asklund, H., L. Ilver, J. Kanski, and J. Sadowski, 2002, Phys. Rev. B 66, 115319.
Auerbach, A., 1994, Interacting Electrons and Quantum Magnetism (Springer, New York).
Baltzer, P. K., P. J. Wojtowicz, M. Robbins, and E. Lopatin, 1966, Phys. Rev. Lett. 151, 367.
von Barth, U., and L. Hedin, 1972, J. Phys. C: Sol. State Phys. 5, 1629.
Berciu, M., and R. N. Bhatt, 2001, Phys. Rev. Lett. 87, 107203.
Berger, L., 1970, Phys. Rev. B 2, 4559.
Berger, L., 1996, Phys. Rev. B 54, 9353.
Bhatt, R. N., M. Berciu, M. P. Kennett, and X. Wan, 2002, J. Supercond. 15, 71.
Bhattacharjee, A. K., G. Fishman, and B. Coqblin, 1983, Physica B+C 117-118, 449.
Bhattacharjee, A. K., and C. B. ŕ la Guillaume, 2000, Solid State Commun. 113, 17.
Blinowski, J., and P. Kacman, 2003, Phys. Rev. B 67, 121204.
Bloembergen, N., and T. J. Rowland, 1955, Phys. Rev. 97, 1679.
Bouzerar, G., T. Ziman, and J. Kudrnovský, 2005a, Europhys. Lett. 69, 812.
Bouzerar, G., T. Ziman, and J. Kudrnovský, 2005b, Phys. Rev. B 72, 125207.
Brey, L., and G. Gómez-Santos, 2003, Phys. Rev. B 68, 115206.
Brey, L., and F. Guinea, 2000, Phys. Rev. Lett. 85, 2384.
Brey, L., C. Tejedor, and J. Fernández-Rossier, 2004, Appl. Phys. Lett. 85, 1996.
Burkov, A. A., and L. Balents, 2003, Phys. Rev. Lett. 91, 057202.
Chapman, R. A., and W. G. Hutchinson, 1967, Phys. Rev. Lett. 18, 443.
Chazalviel, J. N., 1975, Phys. Rev. B 11, 3918.
Chiba, D., F. Matsukura, and H. Ohno, 2004a, Physica E 21, 966.
Chiba, D., Y. Sato, T. Kita, F. Matsukura, and H. Ohno, 2004b, Phys. Rev. Lett. 93, 216602.
Chiba, D., K. Takamura, F. Matsukura, and H. Ohno, 2003a, Appl. Phys. Lett. 82, 3020.
Chiba, D., M. Yamanouchi, F. Matsukura, and H. Ohno, 2003b, Science 301, 943.
Chien, L., and C. R. Westgate, 1980, The Hall Effect and Its Applications (Plenum, New York).
Chow, W. W., and S. W. Koch, 1999, Semiconductor-Laser Fundamentals (Springer-Verlag, Berlin).
Chudnovskiy, A. L., and D. Pfannkuche, 2002, Phys. Rev. B 65, 165216.
Coey, J. M. D., M. Viret, and S. von Molnár, 1999, Adv. Phys. 48, 167.
Craco, L., M. S. Laad, and E. Müller-Hartmann, 2003, Phys. Rev. B 68, 233310.
Das Sarma, S., E. H. Hwang, and A. Kaminski, 2003, Phys. Rev. B 67, 155201.
Das Sarma, S., E. H. Hwang, and D. J. Priour Jr, 2004, Phys. Rev. B 70, 161203(R).
Degiorgi, L., 1999, Rev. Mod. Phys. 71, 687.
Dietl, T., 2001, Acta Phys. Polon. A 100, 139.
Dietl, T., 2002, Semicond. Sci. Technol. 17, 377.
Dietl, T., A. Haury, and Y. M. d’Aubigne, 1997, Phys. Rev. B 55, R3347.
Dietl, T., J. König, and A. H. MacDonald, 2001a, Phys. Rev. B 64, 241201.
Dietl, T., F. Matsukura, and H. Ohno, 2002, Phys. Rev. B 66, 033203.
Dietl, T., H. Ohno, and F. Matsukura, 2001b, Phys. Rev. B 63, 195205.
Dietl, T., H. Ohno, F. Matsukura, J. Cibert, and D. Ferrand, 2000, Science 287, 1019.
Doniach, S., 1977, Physica B+C 91, 231.
Dugaev, V. K., P. Bruno, M. Taillefumier, B. Canals, and C. Lacroix, 2005, Phys. Rev. B 71, 224423.
Durst, A. C., R. N. Bhatt, and P. A. Wolff, 2002, Phys. Rev. B 65, 235205.
Dyck, J. S., C. Drašar, P. Lošťák, and C. Uher, 2005, Phys. Rev. B 71, 115214.
Dyck, J. S., P. Hájek, P. Lošťák, and C. Uher, 2002, Phys. Rev. B 65, 115212.
Eid, K. F., M. B. Stone, K. C. Ku, P. Schiffer, and N. Samarth, 2004, Appl. Phys. Lett. 85, 1556.
Erwin, S. C., and A. G. Petukhov, 2002, Phys. Rev. Lett. 89, 227201.
Erwin, S. C., and I. Zutic, 2004, Nature Materials 3, 410.
Fernández-Rossier, J., and L. J. Sham, 2002, Phys. Rev. B 66, 073312.
Fiete, G. A., G. Zaránd, and K. Damle, 2003, Phys. Rev. Lett. 91, 097202.
Fiete, G. A., G. Zaránd, B. Jankó, P. Redliński, and C. P. Moca, 2005, Phys. Rev. B 71, 115202.
Filippetti, A., N. A. Spaldin, and S. Sanvito, 2005, Chemical Physics 309, 59.
Fleurov, V. N., and K. A. Kikoin, 1976, J. Phys. C: Solid State Phys. 9, 1673.
Frey, T., M. Maier, J. Schneider, and M. Gehrke, 1988, J. Phys. C: Solid State Phys. 21, 5539.
Fröhlich, F., and F. R. N. Nabarro, 1940, Proc. Roy. Soc. London A 175, 382.
Frustaglia, D., J. König, and A. H. MacDonald, 2004, Phys. Rev. B 70, 045205.
Fukumura, T., H. Toyosaki, and Y. Yamada, 2005, Semicond. Sci. Technol. 20, S103.
Furdyna, J. K., 1988, J. Appl. Phys. 64, R29.
Gaj, J. A., J. Ginter, and R. R. Galazka, 1978, Phys. Status Solidi (b) 89, 655.
Gate, S. F. N., and S. Register, 2002, Science 296, 2003.
Goodenough, J. B., 1958, J. Phys. Chem. Solids 6, 287.
Graf, T., M. Gjukic, M. S. Brandt, M. Stutzmann, and O. Ambacher, 2002, Appl. Phys. Lett. 81, 5159.
Graf, T., S. T. B. Goennenwein, and M. S. Brandt, 2003b, Phys. Status Solidi B 239, 277.
Gregg, J. F., I. Petej, E. Jouguelet, and C. Dennis, 2002, J. Phys. D: Appl. Phys. 35, R121.
Haldane, F. D. M., 2004, Phys. Rev. Lett. 93, 206602.
Haldane, F. D. M., and P. W. Anderson, 1976, Phys. Rev. B 13, 2553.
Harrison, W., 1980, Electronic Structure and the Properties of Solid (Freeman, San Francisco).
Hayashi, T., Y. Hashimoto, S. Katsumoto, and Y. Iye, 2001, Appl. Phys. Lett. 78, 1691.
Hayashi, T., M. Tanaka, K. Seto, T. Nishinaga, and K. Ando, 1997, Appl. Phys. Lett. 71, 1825.
Hilbert, S., and W. Nolting, 2005, Phys. Rev. B 71, 113204.
Hirakawa, K., S. Katsumoto, T. Hayashi, Y. Hashimoto, and Y. Iye, 2002, Phys. Rev. B 65, 193312.
Hirakawa, K., A. Oiwa, and H. Munekata, 2001, Physica E 10, 215.
Hohenberg, P., and W. Kohn, 1964, Phys. Rev. 136, B864.
Hwang, E. H., and S. Das Sarma, 2005, Phys. Rev. B 72, 035210.
Hwang, E. H., A. J. Millis, and S. Das Sarma, 2002, Phys. Rev. B 65, 233206.
Inoue, J., S. Nonoyama, and H. Itoh, 2000, Phys. Rev. Lett. 85, 4610.
Jaczynski, M., J. Kossut, and R. R. Galazka, 1978, Phys. Status Solidi (b) 88, 73.
Jain, M., L. Kronik, J. R. Chelikowsky, and V. V. Godlevsky, 2001, Phys. Rev. B 64, 245205.
Jaoul, O., I. A. Campbell, and A. Fert, 1977, J. Magn. Magn. Mater. 5, 23.
Jones, R. O., and O. Gunnarsson, 1989, Rev. Mod. Phys. 61, 689.
Jones, W., and N. March, 1973, Theoretical Solid State Physics (Wiley, New York).
Jungwirth, T., W. A. Atkinson, B. Lee, and A. H. MacDonald, 1999, Phys. Rev. B 59, 9818.
Jungwirth, T., J. König, J. Sinova, J. Kučera, and A. H. MacDonald, 2002b, Phys. Rev. B 66, 012402.
Jungwirth, T., J. Mašek, J. Sinova, and A. H. MacDonald, 2003a, Phys. Rev. B 68, 161202(R).
Jungwirth, T., Q. Niu, and A. H. MacDonald, 2002c, Phys. Rev. Lett. 88, 207208.
Kaminski, A., and S. Das Sarma, 2002, Phys. Rev. Lett. 88, 247202.
Kaminski, A., and S. Das Sarma, 2003, Phys. Rev. B 68, 235210.
Kanamori, J., 1959, J. Phys. Chem. Solids 10, 87.
Karplus, R., and J. M. Luttinger, 1954, Phys. Rev. 95, 1154.
Kasuya, T., 1956, Progr. Theoret. Phys. 16, 45.
Kasuya, T., and A. Yanase, 1968, Rev. Mod. Phys. 40, 684.
Kechrakos, D., N. Papanikolaou, K. N. Trohidou, and T. Dietl, 2005, Phys. Rev. Lett. 94, 127201.
Kim, B. W., and A. Majerfeld, 1995, ETRI Journal 17, 17.
Kitchen, D., A. Richardella, and A. Yazdani, 2005, J. Supercond. 18, 23.
Kohn, W., and L. J. Sham, 1965, Phys. Rev. 140, A1133.
König, J., T. Jungwirth, and A. H. MacDonald, 2001a, Phys. Rev. B 64, 184423.
König, J., H. H. Lin, and A. H. MacDonald, 2000, Phys. Rev. Lett. 84, 5628.
Korotkov, R. Y., J. M. Gregie, B. Han, and B. W. Wessels, 2001, Physica B 308, 18.
Kötzler, J., and W. Gil, 2005, Phys. Rev. B 72, 060412(R).
Kronik, L., M. Jain, and J. R. Chelikowsky, 2002, Phys. Rev. B 66, 041203.
Lang, R., A. Winter, H. Pascher, H. Krenn, X. Liu, and J. K. Furdyna, 2005, Phys. Rev. B 72, 024430.
Lawes, G., A. S. Risbud, A. P. Ramirez, and R. Seshadri, 2005, Phys. Rev. B 71, 045201.
Lazarczyk, P., T. Story, M. Arciszewska, and R. R. Galazka, 1997, J. Magn. Magn. Mater. 169, 151.
Lee, B., T. Jungwirth, and A. H. MacDonald, 2002, Semicond. Sci. Technol. 17, 393.
Lee, B. H., T. Jungwirth, and A. H. MacDonald, 2000, Phys. Rev. B 61, 15606.
Lee, T. C., and W. W. Anderson, 1964, Solid State Commun. 2, 265.
Lee, W.-L., S. Watauchi, V. L. Miller, R. J. Cava, and N. P. Ong, 2004, Science 303, 1647.
Leroux-Hugon, P., and A. Ghazali, 1972, J. Phys. C: Solid State Phys. 5, 1072.
Li, J., L. Hu, and S.-Q. Shen, 2005, Phys. Rev. B 71, 241305.
Litvinov, V. I., and V. K. Dugaev, 2001, Phys. Rev. Lett. 86, 5593.
Liu, C., F. Yun, and H. Morko, 2005, J. Mat. Sci:Materials in Elect 16, 555.
Liu, X., Y. Sasaki, and J. K. Furdyna, 2003, Phys. Rev. B 67, 205204.
López-Sancho, M. P., and L. Brey, 2003, Phys. Rev. B 68, 113201.
Luo, X., and R. M. Martin, 2005, Phys. Rev. B 72, 035212.
Luttinger, J. M., 1958, Phys. Rev. 112, 739.
Luttinger, J. M., and W. Kohn, 1955, Phys. Rev. 97, 869.
Mac, W., A. Twardowski, and M. Demianiuk, 1996, Phys. Rev. B 54, 5528.
Máca, F., and J. Mašek, 2002, Phys. Rev. B 65, 235209.
MacDonald, A. H., P. Schiffer, and N. Samarth, 2005, Nature Materials 4, 195.
Mahadevan, P., and A. Zunger, 2003, Phys. Rev. B 68, 075202.
Mahadevan, P., and A. Zunger, 2004, Appl. Phys. Lett. 85, 2860.
Mahadevan, P., A. Zunger, and D. D. Sarma, 2004, Phys. Rev. Lett. 93, 177201.
Mahan, G. D., 1981, Many-Particle Physics (Plenum Press, New York).
Malozemoff, A. P., 1985, Phys. Rev. B 32, 6080.
Marder, M. P., 1999, Condensed Matter Physics (Wiley, New York).
Matsukura, F., H. Ohno, A. Shen, and Y. Sugawara, 1998, Phys. Rev. B 57, R2037.
Matsukura, F., M. Sawicki, T. Dietl, D. Chiba, and H. Ohno, 2004, Physica E 21, 1032.
Mauger, A., and C. Godart, 1986, Phys. Rep. 141, 51.
Mašek, J., 1991, Solid State Commun. 78, 351.
Mašek, J., J. Kudrnovský, and F. Máca, 2003, Phys. Rev. B 67, 153203.
Mašek, J., and F. Máca, 2003, Phys. Rev. B 69, 165212.
Mašek, J., and F. Máca, 2005, Acta Phys. Pol. A 108, 789.
Mašek, J., I. Turek, V. Drchal, J. Kudrnovský, and F. Máca, 2002, Acta Phys. Polon. A 102, 673.
Mašek, J., I. Turek, J. Kudrnovský, F. Máca, and V. Drchal, 2004, Acta Phys. Pol. A 105, 637.
Mayr, M., G. Alvarez, and E. Dagotto, 2002, Phys. Rev. B 65, 241202.
Munekata, H., A. Zaslavsky, P. Fumagalli, and R. J. Gambino, 1993, Appl. Phys. Lett. 63, 2929.
Myers, R. C., A. C. Gossard, and D. D. Awschalom, 2004, Phys. Rev. B 69, 161305.
Nazmul, A. M., T. Amemiya, Y. Shuto, S. Sugahara, and M. Tanaka, 2005, Phys. Rev. Lett. 95, 017201.
Nazmul, A. M., S. Sugahara, and M. Tanaka, 2003, Phys. Rev. B 67, 241308.
Nozieres, P., and C. Lewiner, 1973, Le Journal de Physique 34, 901.
Ohno, H., 1998, Science 281, 951.
Ohno, H., 1999, J. Magn. Magn. Mater. 200, 110.
Ohno, H., and F. Matsukura, 2001, Solid State Commun. 117, 179.
Ohno, H., H. Munekata, T. Penney, S. von Molnár, and L. L. Chang, 1992, Phys. Rev. Lett. 68, 2664.
Onoda, M., and N. Nagaosa, 2002, J. Phys. Soc. Jpn. 71, 19.
Park, J. H., S. K. Kwon, and B. I. Min, 2000, Physica B 281/282, 703.
Pashitskii, E. A., and S. M. Ryabchenko, 1979, Sov. Phys. Solid State 21, 322.
Perdew, J. P., and A. Zunger, 1981, Phys. Rev. B 23, 5048.
Poddar, P., Y. Sahoo, H. Srikanth, and P. N. Prasad, 2005, Appl. Phys. Lett. 87, 062506.
Prellier, W., A. Fouchet, and B. Mercey, 2003, J. Phys.: Condens. Matter 15, R1583.
Ruderman, M. A., and C. Kittel, 1954, Phys. Rev. 96, 99.
Sadowski, J., and J. Z. Domagala, 2004, Phys. Rev. B 69, 075206.
Saito, H., Zayets, V., Yamagata, S., and A. A, 2003, Phys. Rev. Lett. 90, 207202.
Saito, H., S. Yuasa, and K. Ando, 2005, Phys. Rev. Lett. 95, 086604.
Saito, H., W. Zaets, S. Yamagata, Y. Suzuki, and K. Ando, 2002, J. Appl. Phys. 91, 8085.
Sandratskii, L. M., and P. Bruno, 2002, Phys. Rev. B 66, 134435.
Sandratskii, L. M., P. Bruno, and J. Kudrnovský, 2004, Phys. Rev. B 69, 195203.
Sankowski, P., and P. Kacman, 2005, Phys. Rev. B 71, 201303(R).
Sanvito, S., 2003, Phys. Rev. B 68, 054425.
Sanvito, S., G. Theurich, and N. A. Hill, 2002, Journal of Superconductivity 15, 85.
Sanyal, B., O. Bengone, and S. Mirbt, 2003, Phys. Rev. B 68, 205210.
Sapega, V. F., T. Ruf, and M. Cardona, 2001, Phys. Stat. Sol. b 226, 339.
Sato, K., P. H. Dederichs, and H. Katayama-Yoshida, 2003, Europhys. Lett. 61, 403.
Sato, K., and H. Katayama-Yoshida, 2002, Semicond. Sci. Technol. 17, 367.
Schairer, W., and M. Schmidt, 1974, Phys. Rev. B 10, 2501.
van Schilfgaarde, M., and O. N. Mryasov, 2001, Phys. Rev. B 63, 233205.
Schliemann, J., 2003, Phys. Rev. B 67, 045202.
Schliemann, J., J. König, H. H. Lin, and A. H. MacDonald, 2001a, Appl. Phys. Lett. 78, 1550.
Schliemann, J., J. König, and A. H. MacDonald, 2001b, Phys. Rev. B 64, 165201.
Schliemann, J., and A. H. MacDonald, 2002, Phys. Rev. Lett. 88, 137201.
Schneider, J., U. Kaufmann, W. Wilkening, M. Baeumler, and F. Köhl, 1987, Phys. Rev. Lett. 59, 240.
Schrieffer, J. R., and P. A. Wolff, 1966, Phys. Rev. 149, 491.
Shick, A. B., J. Kudrnovský, and V. Drchal, 2004, Phys. Rev. B 69, 125207.
Shono, T., T. Hasegawa, T. Fukumura, F. Matsukura, and H. Ohno, 2000, Appl. Phys. Lett. 77, 1363.
Singley, E. J., R. Kawakami, D. D. Awschalom, and D. N. Basov, 2002, Phys. Rev. Lett. 89, 097203.
Sinitsyn, N. A., Q. Niu, J. Sinova, and K. Nomura, 2005, Phys. Rev. B 72, 045346.
Sinova, J., T. Jungwirth, and J. Černe, 2004a, Int. J. Mod. Phys. B 18, 1083.
Sinova, J., T. Jungwirth, J. Kučera, and A. H. MacDonald, 2003, Phys. Rev. B 67, 235203.
Slater, J. C., and G. F. Koster, 1954, Phys. Rev. 94, 1498.
Śliwa, C., and T. Dietl, 2005, cond-mat/0505126.
Slonczewski, J. C., 1996, J. Magn. Magn. Mater. 159, L1.
Smit, J., 1955, Physica 21, 877.
Souma, S., S. J. Lee, and T. W. Kang, 2005, Int. J. Mod. Phys. B 19, 3151.
Soven, P., 1967, Phys. Rev. 156, 809.
Stewart, G. R., 1984, Rev. Mod. Phys. 56, 755.
Story, T., R. R. Galazka, R. B. Frankel, and P. A. Wolff, 1986, Phys. Rev. Lett. 56, 777.
Sugano, S., and N. Kojima, 2000, Magneto-Optics (Springer-Verlag, New York).
Sundaram, G., and Q. Niu, 1999, Phys. Rev. B 59, 14915.
Szczytko, J., W. Mac, A. Twardowski, F. Matsukura, and H. Ohno, 1999a, Phys. Rev. B 59, 12935.
Talwar, D. N., and C. S. Ting, 1982, Phys. Rev. B 25, 2660.
Tanaka, M., and Y. Higo, 2001, Phys. Rev. Lett. 87, 026602.
Tang, H. X., R. K. Kawakami, D. D. Awschalom, and M. L. Roukes, 2003, Phys. Rev. Lett. 90, 107201.
Tang, J.-M., and M. E. Flatté, 2004, Phys. Rev. Lett. 92, 047201.
Timm, C., 2003, J. Phys.: Condens. Matter 15, R1865.
Timm, C., and A. H. MacDonald, 2005, Phys. Rev. B 71, 155206.
Timm, C., M. E. Raikh, and F. von Oppen, 2005, Phys. Rev. Lett. 94, 036602.
Timm, C., F. Schäfer, and F. von Oppen, 2002, Phys. Rev. Lett. 89, 137201.
Tserkovnyak, Y., G. A. Fiete, and B. I. Halperin, 2004, Appl. Phys. Lett. 84, 5234.
Tsunetsugu, H., M. Sigrist, and K. Ueda, 1997, Rev. Mod. Phys. 69, 809.
Turek, I., J. Kudrnovský, V. Drchal, and P. Weinberger, 2004, J. Phys.: Condens. Matter 16, S5607.
Velický, B., S. Kirkpatrick, and H. Ehrenreich, 1968, Phys. Rev. 175, 747.
Vurgaftman, I., and J. R. Meyer, 2001, Phys. Rev. B 64, 245207.
Vurgaftman, I., J. R. Meyer, and L. R. Ram-Mohan, 2001, J. Appl. Phys 89, 5815.
Wierzbowska, M., D. Sanchez-Portal, and S. Sanvito, 2004, Phys. Rev. B 70, 235209.
Xu, J. L., M. van Schilfgaarde, and G. D. Samolyuk, 2005, Phys. Rev. Lett. 94, 097201.
Yang, S. R. E., and A. H. MacDonald, 2003, Phys. Rev. B 67, 155202.
Yosida, K., 1957, Phys. Rev. 106, 893.
Zaránd, G., and B. Jankó, 2002, Phys. Rev. Lett. 89, 047201.
Zaránd, G., C. P. Moca, and B. Jankó, 2005, Phys. Rev. Lett. 94, 247202.
Zener, C., 1951a, Phys. Rev. 81, 440.
Zener, C., 1951b, Phys. Rev. 82, 403.
Zhao, Y.-J., W. T. Geng, A. J. Freeman, and B. Delley, 2002, Phys. Rev. B 65, 113202.
Zhou, C., M. P. Kennett, X. Wan, M. Berciu, and R. N. Bhatt, 2004, Phys. Rev. B 69, 144419.
Zutic, I., J. Fabian, and S. Das Sarma, 2004, Rev. Mod. Phys. 76, 323.